От размера заказа

Графически зависимость общих затрат за период, связан­ных с размещением и получением заказов, а также с хранением запаса, от размера заказа представлена на рис. 65.

Определим размер заказа (S), при котором минимизируют общие затраты:

С _общ = С _хран + С_зак → min.

или

С _общ = М ∙ Т ∙(S /2) ∙ Р + К ∙(Q/S) → min. (2)

В данном уравнении два управляемых параметра: S — независимая переменная и С_общ — зависимая переменная.

Общие затраты за период,

связанные i размещением

и получением заказов, а так же

с хранением запаса

С _общ, руб. за период

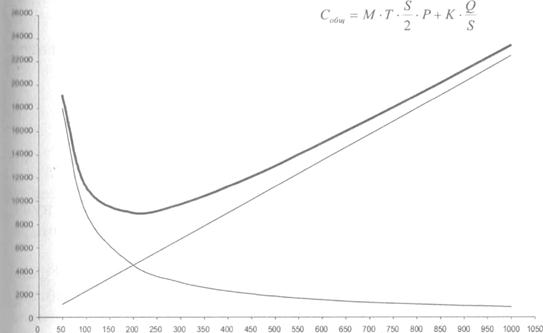
Размер заказа, S, шт.

Рис. 65. Зависимость общих затрат за период, связанных с размещением и получением заказов, а также с хранением запаса, от размера заказа

Остальные параметры являются постоянными коэффици­ентами. В упрощенной форме уравнение (2) примет вид

С _о6щ = a ∙ S + b / S,

где a = (М ∙ Т ∙ Р)/2; b = Q ∙ K.

Функция суммарных затрат имеет минимум в точке, в ко­торой ее первая производная по S равна нулю, а вторая про­изводная больше нуля. Найдем первую производную для С_общ:

С' _общ = a - b/S ².

Найдем значение S, обращающее производную целевой функции в ноль:

a - b/S ² = 0.

Откуда

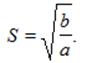(3)

Проверка показывает, что вторая производная больше нуля, следовательно, полученное значение S обеспечивает минимум суммарных затрат на создание запаса и его хранение.

Подставляя в выражение (3) значения а и b, получим формулу, позволяющую рассчитать оптимальный размер заказа, которая в теории управления запасами известна как формула Уилсона:

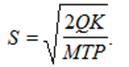(4)

Рассмотрим порядок расчета оптимальных значений осталь­ных управляемых параметров.

Оптимальный размер затрат за период Т на создание за паса (С):

С _{опт.зак} = KQ/S _опт;

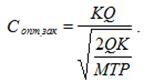
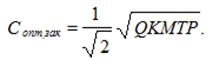(5)

Оптимальный размер затрат за период Т на хранение запаса (С _{опт.хран});

С_{опт.хран}=(М ∙ Т ∙ S /2)∙ Р.

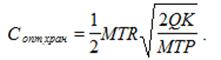
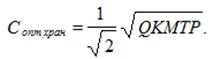(6)

Минимальный (он же оптимальный) размер общих затрат на период на создание и хранение запаса С_{мин.общ}:

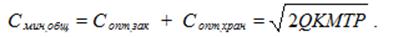
Из формул (5) и (6) следует, что в точке минимума общих затрат затраты на создание запаса за период равны затратам на хранение запаса (за этот же период). Отсюда следует вывод, имеющий существенное практическое значение: если в течение периода затраты, связанные с созданием запаса были равны за­тратам на их хранение, то, значит, товары закупались оптималь­ными, т. е. правильными по размеру партиями.

Оптимальный размер среднего значения текущего запаса

З_{опт.тек.ср} = S _опт/2.

Оптимальное количество заказов за период (частота завоза)

N _опт = Q/S _опт .

Оптимальный период между поставками

t _опт = T/N _опт.

Полученное значение периода между поставками имеет годовое измерение: год/период; (заказ/период) = (год/заказ), т.е. промежуток между заказами измеряется в годах. На практике период между поставками удобнее измерять в месяцах или днях. Расчётная формула при этом имеет вид

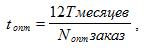
или

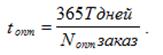
Присвоим неуправляемым параметрам конкретные число­вые величины (табл.12), чтобы иметь возможность на примере показать порядок определения оптимального размера управля­емых параметров.

Таблица 12

Наименование показателя	Обозначение	Ед. измерения	Значение
Спрос на товар за анали-зируемый период	Q	шт/период
Удельные затраты на создание запасов	K	руб.
Удельные расходы по хранению запаса	M	1/год	0,3
Продолжительность анали-зируемого периода в годовом измерении	T	год/период	0,25(один квартал)
Закупочная стоимость единицы товара	P	руб./шт

Оптимальный размер заказываемой партии составит:

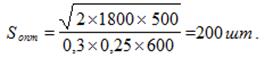
Оптимальный размер затрат за период Т на создание запаса

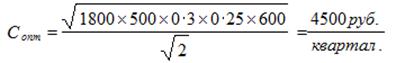
Минимальный (он же оптимальный) размер общих затрат за период на создание и хранение запаса

С_мин.о6щ = 4 500 + 4 500 = 9 000 руб./квартал.

Оптимальный размер среднего значение текущего запаса

З _{опт.тек.ср.} = 200/2 = 100 шт.

Оптимальное количество заказов за период (частота завоза)

N _опт = 1800/200 = 9 заказов/квартал.

Оптимальный период между заказами (рассчитаем этот параметр в днях)

t _опт = 365∙0,25/9 ≈ 10 дней/заказ.

Приведенные выше формулы и расчеты выполнены, исхо­ди из предположения, что потребность в анализируемом периоде, а также размер заказа рассчитываются в натуральном выражении (в штуках). Расчеты не претерпят существенных из­менений, если перейти к денежному выражению потребности и заказа. Приведем пример расчета, исходя из того, что потреб­ность за период в денежном выражении (Q ^ден) составляет:

Q ^ден = (1800шт/период) ∙ (600руб/шт) = 1080 000 руб/период.

Поскольку размер заказа, измеряемый в денежных единицах (S ^ден), равен

S ^ден = SP,

формула для расчёта затрат примет вид

С _хран = (S ^ден/2) ∙ MT.

Внеся соответствующие изменения в формулу (1) и прове­дя последующие преобразования (см. формулы 2, 3 и 4), получим модель для расчета оптимального размера заказа в денежном выражении:

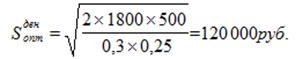
Формулы для расчета остальных управляемых параметром остаются без изменения.

Мы определили для нашего примера оптимальные условии поставок. Игнорирование полученных результатов приведет к завышенным расходам. Например, при завозе товаров не один раз в десять дней по 200 шт., а один раз в месяц по 600 шт. об­щие затраты за период на создание и хранение запаса составят:

С _о6щ = 0,3 ∙(600/2) ∙600 ∙0,25 + 500 ∙(1800/600) = 15000 руб./квартал,

что превышает С _мин.о6щ (9000 руб./квартал) на 2/3.

Дата добавления: 2014-01-03