Определение размера страховых запасов

На рис. 62 представлен идеальный вариант движения запа­са: расход осуществляется равномерно, новая партия поступает на склад точно в момент полного расхода предыдущей. На прак­тике фактический расход запаса неравномерен и может превы­шать плановый. Поступление заказанных товаров по вине по­ставщиков или перевозчиков может запаздывать. В связи с этим предприятия создают страховые запасы. Цель создания страхо­вых запасов — обеспечить непрерывность торгового или производственного процесса в следующих случаях:

• задержка поставщиком срока отгрузки заказа;

• задержка товара в пути при доставке от поставщика;

• непредвиденное возрастание объема сбыта.

Перечисленные ситуации не планируют, но, поскольку они возможны, их ожидают и к ним готовятся, создавая страховые запасы.

Страховой запас позволяет стабильно функционировать и условиях плохо отрегулированных хозяйственных отноше­ний и неизбежных ошибок при прогнозировании и последую­щем планировании спроса.

Страховой запас не является неприкосновенным. Расход этой компоненты общего запаса также неизбежен, как и неиз­бежны погрешности планирования продаж и организации по­ставок. Однако при запланированном ходе поставок и стабиль­ном, соответствующем плану, сбыте величина страхового запа­са, в отличие от текущего, не меняется.

Страховой запас, так же как и текущий, имеет двойственный характер, т. е. играет как положительную, так и отрицательную роль. Значительный страховой запас способен покрыть все слу­чайные отклонения. Предприятие сможет избежать потерь обо­рота и имиджа, вызванных отсутствием в нужный момент запа­сов на складе, т. е. потерь от дефицита. Однако это может при­вести к неоправданно большим затратам на содержание стра­хового запаса на складе компании.

Определяющим экономическим фактором при расчете величины страхового запаса является достижение минимальных суммарных потерь и затрат, вызванных дефицитом и содержанием запаса.

На величину потребности в страховых запасах оказывает влияние следующие основные факторы:

• вероятность того, что поставщик нарушит свои обязательства по отгрузке товаров (по сроку или по количеству, или по тому и другому вместе);

• вероятность незапланированного роста потребности и товарах (роста сбыта);

• вероятность того, что перевозчик нарушит свои обязательства по срокам доставки товаров.

Возможно также влияние других факторов.

Кроме того, на размер страховых запасов влияет характер распределения таких случайных величин, как сроки поставок, объемы сбыта и др.

Существенное влияние на потребность в страховых запасах оказывает допустимая в конкретной ситуации вероятность возникновения дефицита. Например, при снижении допусти мой вероятности дефицита с сорока до одного процента в условиях нормально распределенного спроса потребность в страховых запасах увеличивается более чем в девять раз (в 9,32 раза).

Количественная оценка каждого из перечисленных выше факторов, а также учет их совместного влияния на размер страхового запаса в единой аналитической модели является сложном научной задачей, требующей к тому же обширной информационной поддержки.

Рассмотрим более простую хорошо изученную ситуацию определения оптимального страхового запаса, когда имеется только одна случайная величина, т. е. действует лишь один слу­чайный фактор.

Первый вариант однофакторной ситуации:

• сроки поставок на склад подвержены случайным колеба­ниям;

• сбыт со склада за любой период точно соответствует плану.

Такая ситуация может иметь место, например, для цен­трального склада системы: "центральный склад компании — склады филиалов".

Сроки поставок на центральный склад от поставщиков мо­гут непредсказуемо отклоняться от плановых. Объемы и сроки отгрузок с центрального склада компании на склады филиалов (объемы сбыта) точно определены.

Второй вариант однофакторной ситуации:

• сроки поставок на склад точно соответствуют планам,

• сбыт в периоды между поставками подвержен случайным колебаниям.

В системе "центральный склад компании — склады фи­лиалов" такая ситуация может иметь место на складах фили­алов: внутрисистемные поставки с центрального склада де­терминированы, а сбыт носит неопределенный, стохастиче­ский характер.

Расчет размера страхового запаса по однофакторной ситу­ации, выполняется на основе статистических данных о факти­ческих значениях случайного фактора, например:

• данные о сроках выполнения заказов поставщиком за предшествующие 12 месяцев (вариант 1),

• данные о величине сбыта в периоды между поставками за последние 12 месяцев (вариант 2).

Рассмотрим порядок расчета оптимального размера стра­хового запаса в случае, когда срок и объемы поставок на склад четко соблюдаются, а величина сбыта в периоды между постав­ками имеет случайный характер (вариант 2).

Вначале, пользуясь данными статистического ряда, необ­ходимо определить закон распределения случайной величины. В том случае, если распределение имеет нормальный характер^[53], размер страхового запаса (R) рассчитывают по формуле

R = t σ,

где σ — среднее квадратическое отклонение величины сбыта за периоды поставки;

t — параметр нормального закона распределения (параметр функции Лапласа).

Параметр t определяется на основе решения о допустимой вероятности наличия дефицита (а).

Последовательность определения параметра t:

1) определить оптимальную вероятность возникновения дефицита, величину а;

2) определить значение функции Лапласа F(t) для найденой вероятности возникновения дефицита;

3) определить значение параметра t для найденного значения функции Лапласа F(t).

Остановимся подробнее на характеристике каждого из действий.

1. Определение оптимальной вероятности возникновения дефицита.

Из теории управления запасами известно, что уровень стра­хового запаса R при наличии только одной случайной величи­ны — потребности между двумя смежными поставками — дол­жен быть таким, чтобы вероятность возникновения дефицита (а) определялась выражением

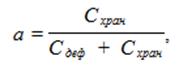
где С_хран — затраты на хранение единицы товара на складе и единицу времени;

С деф — потери из-за дефицита (отсутствия) товара на скла­де в единицу времени.

Например, затраты на хранение единицы товара составляют С_хран = 180 руб./год, а потери от дефицита С_деф = 4320 руб./год

Тогда вероятность возникновения дефицита должна состав­лять^[54]

а = 0,04.

Вероятность возникновения дефицита может быть опреде­лена также из заданного руководством компании или службой маркетинга уровня сервиса η, выраженного в долях от единицы. Тогда

а = 1 - η.

2. Определение значения функции Лапласа F(t) для найден­ной вероятности возникновения дефицита.

График плотности нормального распределения приведен на рис. 66. Напомним, что общая площадь под кривой равна едини­це, т. е. суммарной вероятности всех возможных значений сбы­та. Наибольшую вероятность имеет среднее значение величины сбыта за период поставки. Чем больше отклонение значения сбыта от центра рассеивания, тем меньше вероятность этого со­бытия. Площадь правой заштрихованной области на графике равна допустимой вероятности дефицита (а). Заштрихуем рав­ный участок слева. Площадь оставшейся не заштрихованной ча­сти графика (значение функции Лапласа) находим по формуле

F(t) = 1-2 а.

В нашем примере F(t) = 1 - 2∙0,04 = 0,92.

3. Определение значения параметра t для найденного зна­мения функции Лапласа F(t).

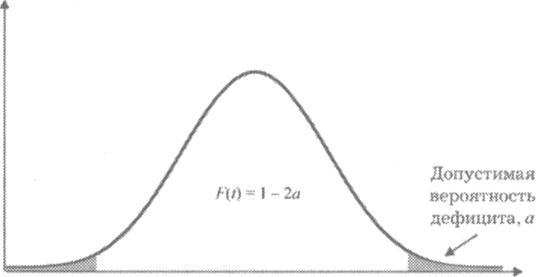
Рис. 66. Плотность нормального распределения

Пользуясь полученным значением функции F(t), по таблицам нормального распределения находим значение аргумента (параметр t).

Значения функции Лапласа, а также соответствующие значения уровня сервиса для некоторых значений t приведены в табл. 14.

В нашем примере t = 1,75.

Таблица 14

Дата добавления: 2014-01-03