Студопедия

КАТЕГОРИИ:

Главная
Случайная страница
Контакты

Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)

При разных значениях t


⇐ Предыдущая12

Значения функции Лапласа и соответствующие значение уровня сервиса

t Параметр функции Лапласа Ф(t) Нормированная функция Лапласа (с округлением до 3-го знака) а Вероятность наличия де­фицита η Уровень сер­виса в долях от единицы η Уровень сервиса в процентах
0,00 0,000 0,50 0,50
0,13 0,103 0,45 0,55
0,25 0,197 0,40 0,60
0,39 0,303 0,35 0,65
0,52 0,397 0,30 0,70
0,53 0,404 0,30 0,70
0,67 0,497 0,25 0,75
0,84 0,599 0,20 0,80
1,04 0,702 0,15 0,85
1,28 0,799 0,10 0,90
1,34 0,820 0,09 0,91
1,41 0,841 0,08 0,92
1,48 0,861 0,07 0,93
1,56 0,881 0,06 0,94
1,65 0,901 0,05 0,95
1,75 0,920 0,04 0,96
1,88 0,940 0,03 0,97
2,05 0,960 0,02 0,98
2,33 0,980 0,01 0,99
2,37 0,982 0,009 0,991 99,1
2,41 0,984 0,008 0,992 99,2
2,45 0,986 0,007 0,993 99,3
2,51 0,988 0,006 0,994 99,4
2,57 0,990 0,005 0,995 99,5

Среднее квадратическое отклонение (σ), входящее в фор­мулу страхового запаса, рассчитывается следующим образом:

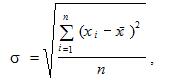
где хi — случайная величина (в нашем примере величина сбыта но время i-й поставки);

х — средняя арифметическая случайной величины;

n — количество значений случайной величины (объем статистики).

Продолжим наш пример и рассчитаем размер страхового запаса. Воспользуемся для этого статистикой значений сбыта в периоды между поставками за последние 12 месяцев (табл. 15).

Таблица 15


⇐ Предыдущая12


Дата добавления: 2014-01-03; Просмотров: 215; Нарушение авторских прав?; Мы поможем в написании вашей работы!

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет


ПОИСК ПО САЙТУ:
Рекомендуемые страницы:

Читайте также:

  1. Акты разных видов
  2. Анализ параллельной работы вентиляторов установленных на разных стволах (связанных между собою горными выработками)
  3. Анализ параллельной работы двух разных вентиляторов методом активизированных характеристик сети.
  4. Анализ параллельной работы двух разных вентиляторов методом суммарных характеристик.
  5. Анализ последовательной работы двух разных вентиляторов методом активизированных характеристик сети
  6. Анализ последовательной работы двух разных вентиляторов методом суммарных характеристик
  7. Атомы разных элементов различаются по массе. Совокупность одинаковых атомов образуют простое вещество, соответствующее определенному химическому элементу.
  8. Влияние некоторых психомоторных качеств и морфофункциональных показателей на результативность в разных видах спорта
  9. Выбор экономически-целесообразных методов амортизации
  10. Горение газообразных, жидких и твердых веществ.
  11. Грамматическая организация фразем в разных языках
  12. Декоративное рисование в разных возрастных группах. Задачи. Основные подходы к проблеме обучения.
studopedia.su - Студопедия (2013 - 2022) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление
Генерация страницы за: 0.001 сек.