Показатели анализа динамики

Динамические ряды могут состоять из какого-то п-го числа варьи­рующих уровней, которые как всякая статистическая совокупность мо­гут быть выражены в тех или иных показателях.

Наиболее распространенные показатели — это абсолютный при­рост или снижение (разность между последующими и предыдущими абсолютными суммарными величинами), темпы роста или снижения (изменения уровня ряда в процентах по сравнению с постоянным ба­зовым показателем или переменным показателем предыдущего уров­ня), среднегодовые темпы прироста или снижения (средняя геометриче­ская величина годовых темпов роста или снижения). Все эти показате­ли подробно рассматривались в относительных и в средних величинах. Поэтому остановимся лишь на некоторых особенностях последнего показателя и на расчете ранее не рассматриваемых величин.

При исчислении среднегодовых темпов прироста (снижения), ко­торые иногда называют средним коэффициентом роста (снижения), необходимо помнить об одной тонкости. Рассматриваемый показатель может быть рассчитан по данным двух позиций: базовой и конечной. Обратимся к реальным сведениям о зарегистрированных преступле­ниях, совершенных на улицах, площадях, в парках и скверах населен­ных пунктов страны за 1991 — 1996 гг. (см. таблицу).

Для расчета среднегодовых темпов снижения рассматриваемых деяний нам достаточно данных за 1991 и 1996 г. Их отношение состав­ляет 89,3%. Среднегодовой темп снижения равняется -2,25%. В дейст­вительности эти деяния по отношению к 1991 г. прирастали в 1992 г. на 23,7%, в 1993 г. - на 35,9%, в 1994 г. - на 15,3%, в 1995 г. - на 9,8% и только в 1996 г. сократились на 10,7%, которые и были приняты в рас­чет, хотя тенденция к снижению обозначилась с 1994 г. Прирост пре­дыдущих лет проигнорирован. В подобных случаях математически точный расчет серьезно расходится с реальным положением дел. По­этому прежде чем рассчитывать среднегодовые темпы прироста (сни­жения), необходимо тщательно проанализировать весь динамический ряд на предмет усреднения темпов изменений. В случае необходимо­сти большие периоды можно разложить на части, для которых расчет средних будет иметь какой-то практический и научный смысл. В на­шем примере желательно рассчитать за 1991-1993 гг. среднегодовые темпы прироста, а за 1993-1996 гг. — среднегодовые темпы снижения. Первые равны +16,55%, а вторые - -18,95%. Сопоставим их с усред­ненным показателем —2,25%. Различия существенны. Для объектив­ности можно рассчитать все эти показатели.

Наряду с указанными показателями в динамическом ряду может быть рассчитан средний уровень ряда. Он применим для любого ряда динамики, интервального и моментного, абсолютных, относительных и средних величин.

Для любых интервальных рядов, для интервальных и моментных рядов средних величин средний уровень ряда рассчитывается по пра­вилам средней арифметической. Например, в Камчатской области было зарегистрировано, разбоев: в 1991 г. — 48, 1992 г. — 64,1993 г. — 100, 1994 г. - 111,1995 г. - 113. Если обозначить годовые уровни сим­волом 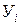, то средний уровень ряда 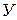может быть исчислен по формуле

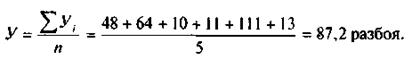
Средний уровень разбоев за 5 лет показателен лишь как некий эта­лон, от которого колеблются реальные показатели. По нему видно, что начиная с 1993 г. годовой уровень разбоев был намного выше среднего. Однако такие расчеты по анализу преступности производятся редко. В практических целях часто важно знать средний уровень нагрузки конкретного следователя (судьи, прокурора, адвоката) за год по меся­цам или за несколько лет при сравнении с общей средней нагрузкой тех или иных работников в целом. В этом случае по предложенной выше формуле рассчитывается средняя нагрузка, скажем, в месяц конкретного работника, а затем — средняя нагрузка на всех работников учреждения. Объективная оценка работы каждого имеет важное значе­ние в управленческой деятельности.

По-иному рассчитывается средний уровень для моментных рядов. Вначале исчисляют средний уровень на начало и на конец периода (на­пример, года), а затем среднюю арифметическую за несколько лет. Эта средняя известна в статистике как средняя хронологическая для момент­ных рядов. Рассмотрим ее на конкретном примере при расчете средне­го уровня арестованных, находящихся в следственных изоляторах страны. Мы располагаем данными о числе арестованных по состоянию на 31 декабря каждого года (в табл. 2 обозначены символом «к» — ко­нец). Эти же данные являются сведениями по состоянию на 1 января следующего года (в таблице обозначены символом «н» — начало).

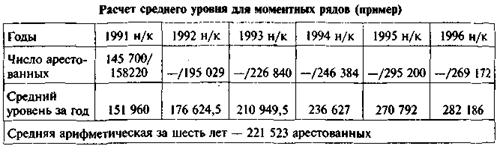
Средний уровень за год и средняя за шесть лет рассчитывались по формуле средней арифметической. Эти же данные можно получить и при разовом расчете:

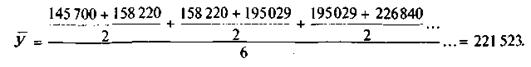
Наличие среднего уровня ряда динамики позволяет рассчитывать среднее квадратическое отклонение отдельных уровней от общей сред­ней 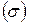, а также коэффициент вариации 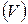. Напомним их формулы:

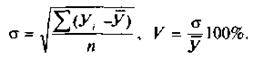
Оперируя этими показателями, особенно в сравнительных иссле­дованиях, можно найти отличительные характеристики, которые при обычных сравнениях сопоставляемых динамических рядов не так оче­видны.

Дата добавления: 2014-01-03