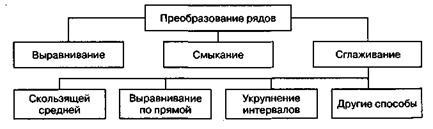
Выравнивание динамических рядов

В судебной статистике не так часто можно встретиться с плав­но меняющимися или неизменными уровнями рядов динамики, осо­бенно в наше сложное в правовом отношении время.

В условиях большой колеблемости показателей динамических ря­дов очень важно выявить три компонента динамики: 1) основные тен­денции, выражающие долговременные изменения; 2) систематиче­ские, но кратковременные изменения; 3) несистематические случай­ные колебания, которые часто обусловлены субъективными и иными частными причинами.

Необходимость отделения наносного, случайного и временного от устойчивого и закономерного в уровнях динамических рядов диктует­ся потребностями изучения основных тенденций и закономерностей развития того или иного явления. С этой целью уровни рядов динами­ки подвергают различным математическим преобразованиям, которые позволяют выявить главные изменения уровней ряда.

Простейшие способы преобразований статистических рядов при формировании вторичных группировок путем сглаживания, укрупне­ния и смыкания рядов, но существует необходимость расширить представле­ния о названных преобразованиях и дополнить их новыми.

Вопрос о смыкании динамических рядов имеет особую актуаль­ность в юридической статистике. Изменение законодательства, прин­ципов и форм учета не позволяют дать единый динамический ряд со­поставимых показателей. Например, некоторое время в УК РСФСР был один перечень тяжких преступлений, в 1994 г. его существенно Расширили, а в 1997 г., после вступления в силу УК 1996 г., принципи­ально изменили. В этих условиях обычный ряд динамики тяжких пре­ступлений за 1991 — 1997 гг. не может быть составлен, так как имею­щиеся данные несопоставимы.

Аналогичные трудности возникают при изменении единиц учета территории и при других основаниях несопоставимости. Чтобы вы­явить общую тенденцию изменения уровня тяжких преступлений можно осуществить смыкание рядов динамики. Покажем это на кон­кретном примере.

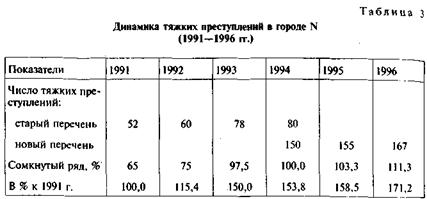
В табл. 3 мы имеем два фактических ряда: один (1991 — 1994 гг.) — по старому перечню тяжких преступлений, другой (1994—1996 гг.) — по новому, расширенному. Для смыкания этих несопоставимых рядов мы принимаем уровень 1994 г. по старому и новому перечню за 100% (за базу), а затем процентируем к ней влево — уровни преступлений по старому перечню и вправо — уровни преступлений по новому перечню (см. сомкнутый ряд). После этого мы можем принять относительный показатель 1991 г. за базу (за 100%) и рассчитать относительные числах новой базе по всем годам. Таким образом мы получили сомкнутый ди­намический ряд, который более или менее точно раскрывает основную тенденцию роста тяжких преступлений в целом.

Сглаживание рядов динамики предполагает приближение их к ос­новной тенденции, к тренду, способами укрупнения интервалов, скользящей средней, выравниванием по прямой, выравниванием по показательной функции, по параболе, при помощи ряда Фурье и другими методами.

Сглаживание рядов динамики путем укрупнения интервалов заклю­чается в определении итоговых или средних показателей для укрупненных интервалов. Обратимся к табл. 4.

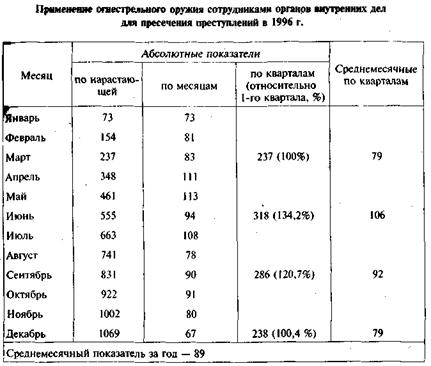
В месячных отчетах МВД России сведения приводятся по нарас­тающей: за январь, январь — февраль, январь — март и т.д. Такие на­копительные данные по применению огнестрельного оружия сотруд­никами органов внутренних дел в целях пресечения преступлений приведены в графе 2 табл. 4. Они не раскрывают динамику, они рас­крывают кумуляту. Помесячные данные (графа 3) показывают то рост, то снижение случаев применения оружия: тенденция неопреде­ленна. Укрупнив месячные данные по кварталам и рассчитав средние показатели за каждый квартал и год в целом, мы обнаруживаем впол­не определенную сезонную тенденцию. В первом квартале число ана­лизируемых случаев минимально (100%), во втором — их уровень достигает апогея (134,2%), в третьем — их число снижается (120,7%), а в четвертом — достигает исходного уровня (100,4%)У Обращение к средним величинам может углубить аналитические возможности ук­рупнения данных. Такие укрупнения интервалов допустимы лишь в интервальных рядах.

В моментных рядах и рядах средних величин укрупнение интерва­лов осуществляется на основе расчета средних уровней по формуле средней арифметической, так как суммирование уровней моментных радов и рядов средних величин недопустимо. В табл. 4 (графа 5) приве­дены средние месячные показатели наблюдаемых случаев в каждом квартале, которые несут ту же информацию о динамике наблюдаемого явления, что и общие суммы за каждый квартал (графа 4). При укруп­нении средних месячных за каждый квартал по правилам средней арифметической мы можем найти среднемесячный показатель за год:

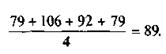
Он равен среднемесячному показателю, полученному путем сло­жения месячных данных и деления полученной суммы на 12 месяцев (см. последнюю строку в таблице).

Следующий способ выявления тенденции развития рядов динами­ки—их сглаживание способом скользящей средней. Для этого необходимо последовательно исчислять среднюю из двух, трех, четырех, пяти и боль­ше уровней. Обратимся к динамике преступности в СССР за 1981—1990 гг., когда изменения преступности были «скачущими» (табл. 5).

Рассчитаем среднюю за первые три года, затем, начиная с 1982 г., за последующие три года, потом, начиная с 1983 г., за следующие три года и т.д.

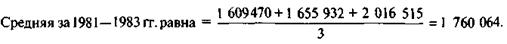
Аналогичным образом рассчитывались средние за последующие трехлетия (см. табл. 5, графу 3). Динамический рад усредненных дан­ных получился более сглаженным, чем реальный, но укороченным на один уровень в начале и на один уровень в конце. Если бы мы усредня­ли по пятилетиям, то рад укоротился бы на два уровня в начале и на два — в конце. Чем больше интервал усреднения, тем более сглажен­ным получается динамический рад и, наоборот, чем меньше интервал, тем ряд получается менее сглаженным.

Третьим видом сглаживания динамического ряда можно назвать выравнивание уровней ряда по прямой. Оно применяется тогда, когда абсолютные приросты более или менее постоянны, т.е. когда уровни ряда изменяются близко к линии арифметической прогрессии.

Уравнение прямой линии выражается формулой 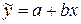, где 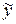— значения уровней выровненного ряда, которые необходимо вычис­лить; а и b — параметры прямой; х — показатели времени (дни, меся­цы, годы).

Выравнивание уровней ряда по прямой заключается в замене фактиче­ских уровней ряда (у) на теоретические ( 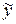), которые вычисляются с помо­щью уравнения прямой линии. Неизвестные нам параметры а и b находят­ся способом наименьших квадратов, представляющим собой систему двух нормальных уравнений (I — знак суммы; п — число уровней): 1) 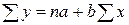, 2) 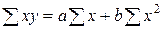. Из этих уравнений определяются а и b. Подроб­ное решение этих уравнений на конкретном примере будет изложено в следующей главе при расчете парного коэффициента корреляции.

Зная значения а и b, мы можем решить уравнение прямой линии 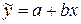для каждого года отдельно (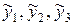и т.д.). Получив теоре­тический ряд чисел, можно изобразить их графически рядом с кривой фактического ряда.

Наряду с рассмотренными способами выравнивания уровней ря­дов динамики существуют и другие более сложные, требующие соот­ветствующей математической подготовки. К ним относятся:

а) выравнивание по показательной функции, которое полезно при изменении уровней ряда в геометрической прогрессии;

б) выравнивание по параболе;

в) выравнивание при помощи ряда Фурье.

Эти методы применяются тогда, когда фактические уровни ряда динамики имеют периодические изменения, например, сезонную вол­ну, которую можно наблюдать в динамике преступности и других юри­дически значимых явлений.

Необходимость выравнивания рядов динамики в юридической статистике требуется, главным образом, при прогнозировании мето­дом экстраполяции (продолжения выявленного тренда на будущее) преступности и ее отдельных групп и видов, при составлении планов и программ борьбы с преступлениями и правонарушениями, при опре­делении возможной нагрузки оперативных работников и в других слу­чаях. Выравнивание рядов может также использоваться при нахожде­нии недостающих данных методом интерполяции (продолжения вы­явленного тренда на прошлое).

Заключительная часть. Подводятся итоги лекции. Даются ответы на вопросы студентов, возникшие в ходе лекции.

Выдаётся задание студентам на самостоятельную работу:

Повторить материал данной лекции. Быть готовым к ответам на следующие вопросы:

1. Дайте определение ряда динамики,

2. Назовите и поясните основные показатели ряда динамики.

3. Поясните, что показывают начальный, средний и конечный уровни ряда.

4. Приведите примеры интервальных и моментных рядов, поясните отличия.

5. Что называют абсолютным приростом (снижением)?

6. Как определяются темпы роста (снижения)?

7. Раскройте смысл среднегодовых темпов прироста (снижения).

8. Назовите основные способы преобразования рядов динамики.

9. Поясните метод сглаживания рядов динамики.

10. Как осуществляется сглаживание способом скользящей средней?

11. Каким образом выравнивают уровни ряда по прямой?

Дата добавления: 2014-01-03