Формула Тейлора

Предположим, что функция 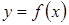имеет все производные до 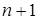порядка в некотором промежутке, содержащем точку a. Из определения дифференцируемости функции имеем 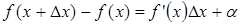, где 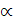- бесконечно малая функция. Возьмем в этом выражении x за a, и запишем в виде 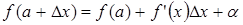. Т.к. 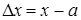, то

.

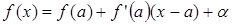Если пренебречь 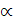- бесконечно малой функцией, то получим формулу для приближенного вычисления функции

.

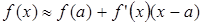В правой части стоит многочлен первой степени по степеням 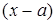. Очевидно, что этот многочлен близок к 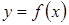и совпадает с функцией в точке 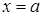. Найдем аналогичный полином n- ой степени и оценим, на сколько он отличается от .

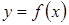Предположим, что

,

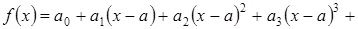
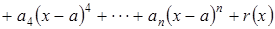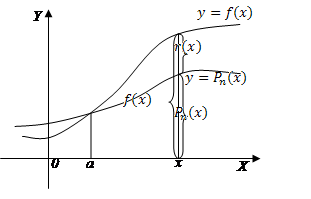где 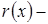остаточный член, показывающий отличие 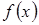от многочлена 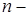ой степени в правой части формулы. Определяем коэффициенты этого многочлена. Полагаем 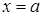. Тогда 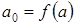при выполнении условия 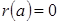. Дифференцируем эту функцию поочередно 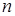раз, тогда

,

,

,

,

……………………………….

.

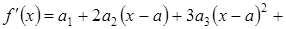
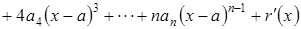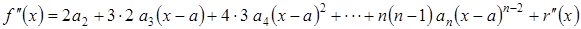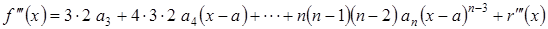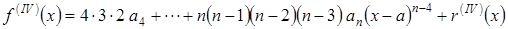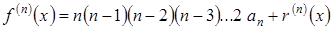Подсчитаем вычисленные производные при 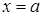. При выполнении условий 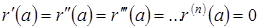из формулы для первой производной имеем 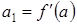, из формулы для второй производной следует 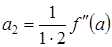, формула для третьей и четвертой производных приводит к

, ,… .

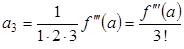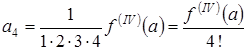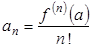Подставляем полученные коэффициенты в формулу, в результате

.

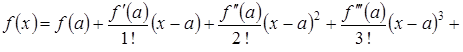
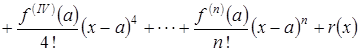Проанализируем, что следует из условий, налагаемых на остаточный член. Из условия 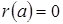следует, что 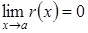, то есть 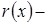бесконечно малая при 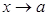. Поскольку 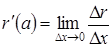, где ,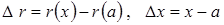

,

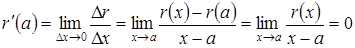следовательно, при 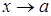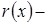бесконечно малая, более высокого порядка малости, чем 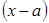. Совершая аналогичную процедуру с остальными условиями на производные остаточного члена, выясняем, что в вышеприведенной формуле остаточный член при 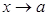является бесконечно малой, более высокого порядка малости, чем 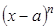. Тогда

.

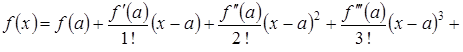
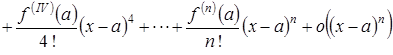Такое представление остаточного члена показывает, что остаточный член есть бесконечно малая, более высокого порядка малости, чем .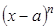

Полученная формула используется для приближенного вычисления значения функции с помощью полинома. Имеется несколько вариантов остаточных членов, более приспособленных для установления количества сохраняемых в формуле членов, обеспечивающих наперед заданную точность приближенного вычисления (аппроксимации) функции. Сведения о них имеются в литературе, указанной в списке. Приведем лишь остаточный член в форме Лагранжа

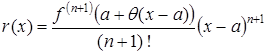, где .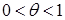

Широко используется частный случай формулы Тейлора – формула Маклорена

,

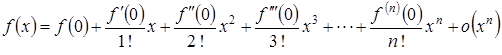представляющая разложение функции в окрестности нулевой точки.

Так же формулу Тейлора можно записать через дифференциалы:

.

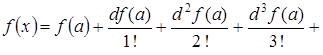
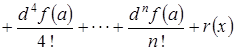Пример 1. Рассмотрим функцию 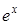. Нетрудно заметить, что любая производная этой функции равна самой функции, а 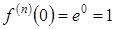. В соответствии с формулой Маклорена

.

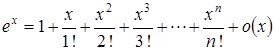Пример 2. Рассмотрим функцию 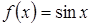. Очевидно, 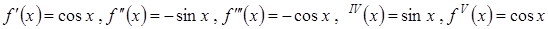и т.д.

Тогда

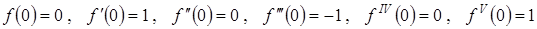и т. д.

Первые члены формулы Маклорена принимают вид

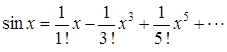
Анализируя первые члены разложения, записываем его общий член 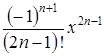. В результате

.

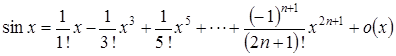Пример 3. Получим разложение по формуле Маклорена функции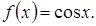

, .

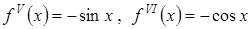Очевидно

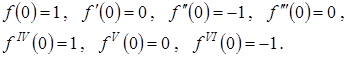
В соответствии с формулой Маклорена получаем

.

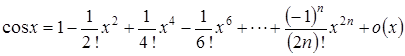Замечание. Суммирование в формулах Маклорена для 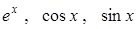начинается с 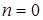, при этом считается .

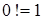Приложения производной функции

Дата добавления: 2014-01-03