
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи синтеза и анализа. Оптимальное проектирование конструкций
|
|
|
|
Проектирование — сложный и трудно формализуемый процесс, объединяющий такие важные процедуры, как синтез структуры, выбор параметров элементов, анализ и принятие решения. Особенно важна начальная стадия проектирования, когда выбираются эффективный физический принцип действия, рациональное техническое решение и определяются оптимальные значения параметров.
Задачи синтеза и анализа. Под синтезом понимаются проектные процедуры, направленные на получение новых описаний проектируемого объекта в соответствии с заданными показателями его функционирования. Анализ — это проектные процедуры, имеющие целью получение информации о свойствах проектируемого объекта по заданному его описанию.
Задачи синтеза связаны с созданием проектных документов и самого проекта, а задачи анализа связаны с оценкой проектных документов.
Процедуры синтеза делятся на процедуры структурного и параметрического синтеза.
Поиск рационального технического решения при выбранном физическом принципе действия осуществляется методами структурного синтеза. Определение оптимальных значений параметров элементов технической системы известной структуры представляет собой задачу параметрического синтеза, или параметрической оптимизации.
Целью структурного синтеза является определение структуры объекта — перечня типов элементов, составляющих объект, и способа связи элементов между собой в составе объекта.
Параметрический синтез заключается в определении числовых значений параметров элементов при заданных структуре и условиях работоспособности, влияющих на выходные параметры объекта, т. е. при параметрическом синтезе нужно найти точку или область в пространстве внутренних параметров, в которых выполняются те или иные условия (обычно условия работоспособности).
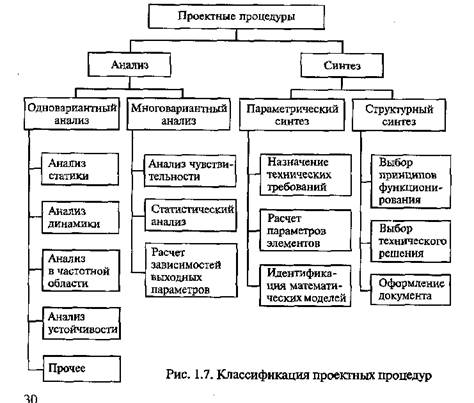
Классификация проектных процедур приведена на рис. 1.7.
|
Процедуры анализа делятся на процедуры одно- и многовариантного анализа.
При одновариантном анализе заданы значения внутренних и внешних параметров, требуется определить значения выходных параметров объекта. Удобно использовать геометрическую интерпретацию этой задачи, связанную с понятием пространства внутренних параметров; это я-мерное пространство, в котором для каждого из п внутренних параметров х,- выделена координатная ось. При одновариантном анализе задается также некоторая точка в пространстве внутренних параметров и требуется в этой точке определить значения выходных параметров. Подобная задача обычно сводится к однократному решению уравнений, составляющих математическую модель, что и обусловливает название данного вида анализа.
Многовариантный анализ заключается в исследовании свойств объекта в некоторой области пространства внутренних параметров. Такой анализ требует многократного решения систем уравнений (многократного выполнения одновариантного анализа).
Синтез называется оптимизацией, если определяются наилучшие в заданном смысле структура и значения параметров. При расчетах оптимальных значений параметров при заданной структуре говорят о параметрической оптимизации. Задачу выбора оптимальной структуры называют структурной оптимизацией.
Постановка задачи оптимизации имеет содержательный смысл только в том случае, когда появляется необходимость выбора одного из конкурирующих вариантов, полученных при ограниченности ресурсов. Техническое проектирование всегда ведется в условиях жестких ограничений на материальные, энергетические, временные и прочие виды ресурсов. Вместе с тем средства САПР позволяют выполнить разработку нескольких альтернативных вариантов, поэтому окончательный выбор технического объекта (принятие решения) необходимо проводить с учетом выработанных правил предпочтения на основании установленных критериев. Выбор критерия является одним из важных этапов постановки задачи оптимизации, так как все последующие действия направлены на поиск объекта, наиболее близкого к оптимальному по выбранному критерию.
В основе построения правила предпочтения лежит целевая функция, количественно выражающая качество объекта и потому называемая также функцией качества, или критерием оптимальности. Формирование целевой функции всегда выполняется с учетом различных выходных параметров проектируемого устройства. В зависимости от содержательного смысла этих параметров и выбранного способа их сочетания в целевой функции качество объекта будет тем выше, чем больше ее значение (максимизация) или чем меньше ее значение (минимизация).
Выбор целевой функции носит субъективный характер, и поэтому объект может быть оптимален только в смысле данного критерия.
В большинстве подходов к оценке технического объекта принято ориентироваться на эталонные образцы, на мнение ведущих специалистов отрасли (экспертные оценки) или на технико-экономические показатели, определяемые техническим заданием (ТЗ) на проектирование. При подготовке ТЗ обычно учитываются достижения, полученные в мировой практике, а также в той или иной мере экспертные оценки, поэтому более объективной следует считать ориентацию на ТЗ. Наиболее полная оценка проектных решений может быть выполнена на основе анализа технико- экономических показателей с учетом требований, сформулированных в ТЗ.
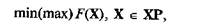
|
Качество функционирования любой системы характеризуется вектором выходных параметров Y = (Y1,Y2…..Yn)- Некоторые из выходных параметров могут быть измерены количественно, другие представляют собой качественную сторону объекта, поэтому все выходные параметры обычно делят соответственно на количественные и качественные. В дальнейшем под вектором Y будем подразумевать вектор количественных параметров.
К выходным параметрам, определяющим качество автомобиля или трактора, можно отнести тяговые и скоростные характеристики, показатели разгонной и тормозной динамики, управляемости и устойчивости, комфортабельности, расход топлива, количественный и качественный состав загрязняющих веществ, выбрасываемых в атмосферу с выхлопными газами, и многие другие. Значение целевой функции может возрастать или убывать с увеличением качества выходного параметра, поэтому в первом случае необходимо искать максимум, а во втором — минимум целевой функции.
Каждый из составляющих вектор Y выходных параметров зависит от множества внутренних параметров проектируемого объекта. Следует отметить, что значения некоторых внутренних параметров назначаются и не подлежат изменению. К таким параметрам, например, можно отнести параметры унифицированных элементов или те из них, значения которых оговорены в техническом задании на проектирование. Остальные параметры можно выбрать, ориентируясь на прототипы с учетом собственного опыта и оценки возможных перспектив развития конструкций подобных объектов.
Внутренние параметры, значения которых могут меняться в процессе оптимизации и которые являются аргументами целевой функции, называют управляемыми параметрами.
Пусть в проектируемом объекте имеется n управляемых параметров, образующих вектор X = (х1 х2,..., хn). Обозначим целевую функцию через F(X), а область ее определения — через ХР. Вектор X определяет координаты точки в области определения ХР. Если элементы вектора X принимают только дискретные значения, ХР является дискретным множеством точек и задача оптимизации относится к области дискретного (в частном случае целочисленного) программирования.
Большинство задач параметрической оптимизации технических объектов формулируется в терминах непрерывных параметров. Если экстремум целевой функции ищется в неограниченной области ХР, его называют безусловным, а методы поиска — методами безусловной оптимизации. Если экстремум целевой функции ищется в ограниченной области ХР, его называют условным.
Для решения задач проектирования в машиностроении характерны методы условной оптимизации.
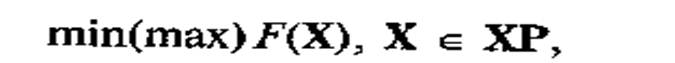
|
Таким образом, задачу поиска оптимального решения можно в общем случае сформулировать следующим образом:
где X — вектор управляемых параметров; F(X) — целевая функция; ХР — область допустимых значений вектора управляемых параметров.
Постановка задачи оптимизации. Основная проблема постановки задачи оптимизации заключается в выборе целевой функции. Сложность выбора целевой функции состоит в том, что любой технический объект первоначально имеет векторный характер критериев оптимальности (многокритериальность), причем улучшение одного из выходных параметров, как правило, приводит к ухудшению другого, так как все выходные параметры являются функциями одних и тех же управляемых параметров и не могут изменяться независимо друг от друга. Такие выходные параметры называют конфликтными.
Целевая функция должна быть одна (принцип однозначности). Сведение многокритериальной задачи к однокритериальной называют сверткой векторного критерия. Задача поиска его экстремума сводится к задаче математического программирования.
В зависимости от того, каким образом выбираются и объединяются выходные параметры в скалярной функции качества, различают частные, аддитивные, мультипликативные, минимаксные, статистические критерии и т.д.
Частные критерии могут применяться в случаях, когда среди выходных параметров можно выделить один основной параметр У/(Х), наиболее полно отражающий эффективность проектируемого объекта; этот параметр принимают за целевую функцию. Различные группы и категории транспортных и тяговых средств очень сильно отличаются по назначению (например, тракторы, грузовые автомобили и спортивные автомобили), поэтому для них в качестве выходных параметров, применимых как целевая функция, могут быть и грузоподъемность, и расход топлива, и динамические качества, и многие другие. Условия работоспособности объекта по всем остальным выходным параметрам относят при этом к функциональным ограничениям. Оптимизация на основе такой постановки называется оптимизацией по частному критерию.
Достоинство такого подхода — его простота, а существенный недостаток — то, что возможно получить высокое качество объекта только по тому параметру, который принят в качестве целевой функции, в то время как остальные выходные параметры будут только приемлемыми.
Теоретически возможен следующий подход. Можно выбрать один, наиболее значимый выходной параметр и провести его оптимизацию. Затем выбрать следующий по значимости параметр и провести его оптимизацию при условии, что значения управляемых параметров, входящие в выражение как для первого, так и для второго выходных параметров, при оптимизации второго параметра должны быть зафиксированы на уровне, достигнутом при оптимизации первого параметра, а оптимизация должна проводиться только с использованием управляемых параметров, не вошедших в описание выходного параметра, оптимизируемого первым. Далее по такому же принципу можно оптимизировать и все остальные выходные параметры. Однако это возможно только в тех случаях, когда выходные параметры зависят хотя бы частично от различных наборов управляемых параметров, что на практике бывает далеко не всегда.
Взвешенный аддитивный критерий применяют тогда, когда условия работоспособности позволяют выделить две группы выходных параметров. В первую группу входят выходные параметры ^(Х), значения которых в процессе оптимизации нужно увеличивать (производительность, вероятность безотказной работы, для транспортных средств — грузоподъемность, максимальная скорость и т.п.), во вторую — выходные параметры yf(X), значения которых следует уменьшать (расход топлива, масса транспортного средства, время разгона и пр.).
В этом случае целевая функция свертки будет иметь вид:
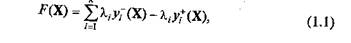
где λi > 0 — весовой коэффициент, определяющий степень важности i-го выходного параметра (обычно значения λi; выбираются проектировщиком и в процессе оптимизации остаются постоянными).
Объединение нескольких выходных параметров, имеющих в общем случае различную физическую размерность и величину, в одной скалярной целевой функции требует предварительного нормирования этих параметров. Способы нормирования параметров могут быть различны. Наиболее простым является отнесение этого параметра к некоторой заранее заданной средней величине, определяемой из опыта предыдущего проектирования, или к допускаемой величине (например, допускаемые напряжения). В этом случае все составляющие выражения (1.1) будут безразмерными величинами одного порядка, что делает удобным манипулирование коэффициентами λi в процессе проектирования.
Наиболее типичным случаем параметрической оптимизации технических объектов является поиск значений вектора управляемых
параметров X, определяющих экстремум целевой функции при наличии ограничений. Для дальнейшего изложения будем считать, что в процессе оптимизации ищется минимум целевой функции. Таким образом, задачу поиска оптимального решения можно в общем случае сформулировать следующим образом:
min F(Х) (1.2)
Здесь X е ХР при прямых ограничениях xHi < xi < хВi- для любого I e [1, я], где xHh xBi— максимально и минимально допустимые значения i-го управляемого параметра; п — размерность пространства управляемых параметров и при функциональных ограничениях.
Функциональные ограничения, как правило, представляют собой условия работоспособности выходных параметров, не вошедших в целевую функцию, и могут быть:

где у(Х) и ф(Х) — вектор функции.
Выбор метода решения зависит от способа постановки задачи оптимизации.
Любая из точек X е ХР является допустимым решением задачи. Часто параметрический синтез ставится как задача определения любого из допустимых решений. Однако гораздо важнее решить задачу оптимизации — найти оптимальное решение среди допустимых.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 11817; Нарушение авторских прав?; Мы поможем в написании вашей работы!