Методы решения задач оптимизации

Расчет выходных параметров объекта в САПР, как правило, выполняется через численное решение систем алгебраических и дифференциальных уравнений. Целевая функция и функциональные ограничения определяются неявным образом, что не позволяет оценить их свойства (выпуклость, вогнутость и т.д.) с приемлемыми затратами вычислительных ресурсов. Поэтому решение задач оптимизации в САПР ведется с помощью поисковых методов математического программирования, использующих предшествующую информацию для построения улучшенного решения задачи, т. е. эти методы являются итерационными.

По ряду признаков задачи поиска экстремума могут быть отнесены к тому или иному классу. Большинство постановок задач параметрической оптимизации технических систем сводятся к задачам нелинейного программирования, так как целевая функция

и ограничения описываются нелинейными зависимостями от вектора управляемых параметров. В отдельных случаях при проектировании удается так сформулировать задачу, что целевая функция и ограничения являются линейными функциями своих аргументов. Тогда имеет место задача линейного программирования. В зависимости от типа искомого экстремума различают методы локальной и глобальной, условной и безусловной оптимизации. Практически используемые методы в основном являются методами локального поиска.

Одновременно надежные и экономичные методы поиска глобального экстремума в настоящее время неизвестны. Надежным, но крайне неэкономичным методом глобального поиска является метод сканирования. При его применении область определения F(Х) в пространстве управляемых параметров разбивается на к подобластей, в центре каждой из которых вычисляется значение целевой функции. Если функция зависит от п параметров, необходимо выполнить к" вариантов расчетов. Чтобы получить достоверную картину поведения гиперповерхности отклика целевой функции, необходимо сканировать допустимую область с достаточно малым шагом, поэтому даже для сравнительно несложных задач затраты машинного времени на поиск становятся недопустимо большими. Этот недостаток характерен и для методов случайного поиска глобального экстремума. Однако затраты ресурсов на случайный поиск можно сделать приемлемыми, если не предъявлять высоких требований к надежности определения экстремума.

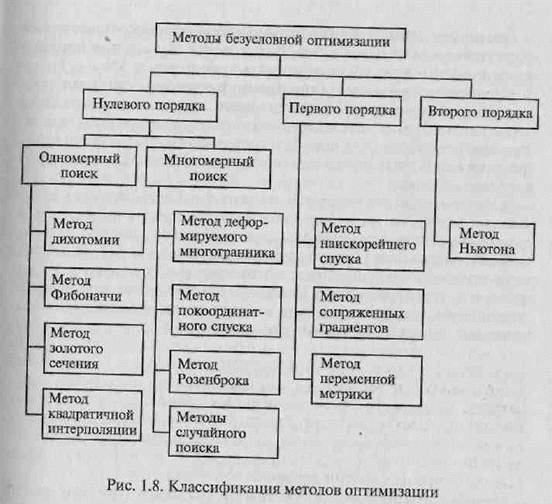
Наиболее многочисленную группу составляют методы безусловной оптимизации. Некоторое представление о широко применяемых методах этой группы дает рис. 1.8.

В зависимости от порядка используемых производных целевой функции по управляемым параметрам методы безусловной оптимизации делят на методы нулевого, первого и второго порядков.

В методах нулевого порядка (прямых методах) информация о производных не используется. Для методов первого порядка необходимо вычислять как значение функции качества, так и ее первые частные производные (градиентные методы). В методах второго порядка организация поиска экстремума ведется с учетом значений целевой функции, ее первых и вторых производных.

В зависимости от количества управляемых параметров целевой функции различают методы одномерного и многомерного поиска. Одномерный поиск может рассматриваться как самостоятельная задача, если аргументом целевой функции является один параметр. Такой же поиск используется в качестве части процедуры многомерной оптимизации в тех случаях, когда необходимо найти оптимальный шаг в выбранном направлении.

Задача условной оптимизации может быть сформулирована как задача безусловной оптимизации с помощью методов Лагранжа или штрафных функций. Тогда для ее решения применяются методы безусловной оптимизации.

Задача условной оптимизации может быть решена и методами условной оптимизации (методы проекции градиента, допустимых направлений и др.).

Практически во всех методах оптимизации стремятся построить такую последовательность значений X₀, X₁ X₂,..., при которой F(Хо) > F(Х₁) > F(Х2) >... В этом случае обеспечивается сходимость результатов и можно надеяться, что минимум функции будет найден.

Важной характеристикой методов является их скорость сходимости. Однако оценка сходимости того или иного метода обычно базируется на некоторых теоретических предпосылках относительно особенностей целевой функции (например, функция дважды непрерывно дифференцируема или сильно выпукла) и зависит от выбора начальной точки поиска. Теоретические предпосылки относительно реальных целевых функций могут не удовлетворяться, поэтому скорость сходимости в этих случаях можно рассматривать как сравнительную оценку метода.

Численные методы поиска оптимума позволяют построить последовательность шагов от начальной точки X_o через некоторые промежуточные точки Хк к локальному экстремуму X*.

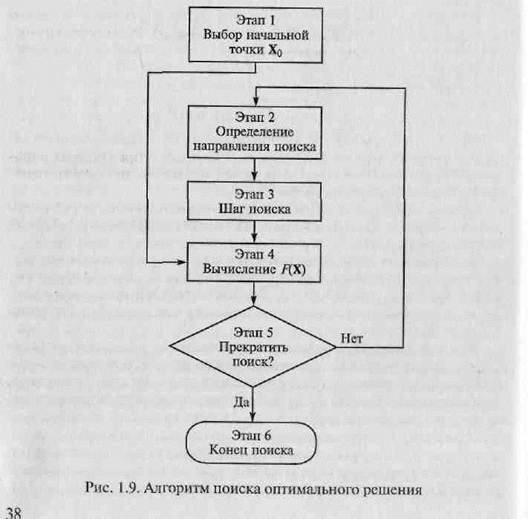
Схема алгоритма поиска оптимального решения для общего случая показана на рис. 1.9.

Как отмечалось выше, выбор исходной точки поиска X₀ ВО МНОГОМ определяет успех решения всей задачи. Очевидно, что X₀ должна принадлежать области определения целевой функции и, чем ближе к экстремуму выбрана X₀, тем быстрее и с большей вероятностью экстремум будет найден. Сущность метода оптимизации определяется этапами 2 и 3 алгоритма, на которых выбирается направление дальнейшего поиска и вычисляются координаты очередной точки Х_k+1 на траектории поиска. Далее в точке _{Хk+ 1} вычисляются значения целевой функции F(Х_k+1) и функций-ограничений, т.е. определяется информация, позволяющая судить о достигнутом успехе. Инженер может назначить различные условия прекращения поиска, и, в зависимости от степени их выполнения, поиск будет продолжен или прекратится.

Методы одномерного поиска строятся в предположении унимодальности (одноэкстремальности) функции F(x) на заданном интервале [а, Ь]. К функции не предъявляются требования дифференцируемости или непрерывности. Предполагается, что для любого х е [а, Ь] значение F(x) может быть вычислено, т.е. найдено путем вычислительного эксперимента.

Методы одномерного поиска можно разделить на методы последовательного поиска (методы дихотомии или половинного деления, Фибоначчи и золотого сечения) и методы, использующие аппроксимацию функции (методы квадратичной и кубической интерполяции и др.).

Для большинства задач, связанных с поиском оптимальных решений при проектировании таких сложных технических систем, как автомобиль и трактор, методы одномерного поиска практически не применимы, поскольку выходные параметры этих машин, как правило, зависят от множества управляемых параметров. Обычно в этом случае применяются методы многомерного поиска.

В качестве примера многомерного поиска рассмотрим метод покоординатного спуска (метод Гаусса—Зейделя). Рассмотрим функцию двух переменных, поскольку в этом случае возможна геометрическая интерпретация рассматриваемого метода.

Таким образом, необходимо решить задачу

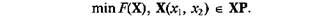
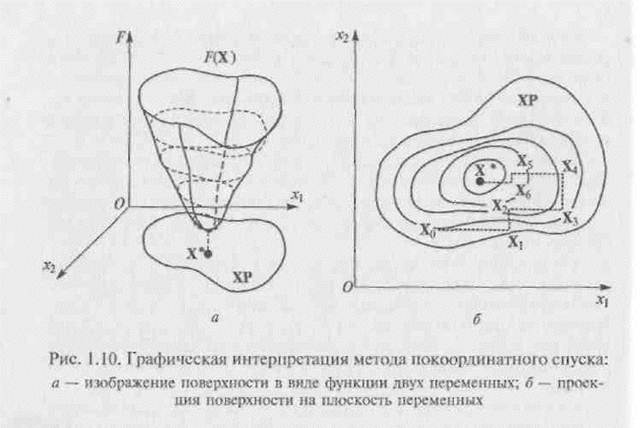
На рис. 1.10, а изображена поверхность, представляющая собой изображение функции F(X) двух переменных (управляемых параметров) х1 и х2. Проекция этой поверхности на плоскость переменных Х1 и х2 показана на рис. 1.10, б.

В соответствии с алгоритмом, приведенным на рис. 1.9, на плоскости управляемых параметров Х1Ох2 выберем начальную точку X₀ с координатами (х10; х20) и определим для нее значение целевой функции F0. Затем, в соответствии с указанным алгоритмом, выберем направление поиска. Для этого зафиксируем значение управляемого параметра х2 = х20 = const, а значение управляемого параметра Х1 = х10 изменим на величину заранее выбранного шаг Для полученной пары значений управляемых параметров вычислим значение целевой функции. Если полученное значение целевой функции будет больше первоначального, необходимо изменить значение управляемого параметра Хm на величину шага в противоположном направлении и для этой точки снова вычислить значение целевой функции. Направление выбирается с таким расчетом, чтобы значение целевой функции стало меньше первоначального. Далее в выбранном направлении продолжаем перемещение с выбранным шагом до тех пор, пока значение целевой функции уменьшается. При нарушении этого условия зафиксируем достигнутое на предыдущем шаге значение управляемого параметра Х1 (точка X1), а затем начинаем перемещение в направлении управляемого параметра х2 с определенным шагом, пользуясь закономерностями, описанными выше, до точки Х2, в которой достигнут минимум целевой функции.

После этого зафиксируем значение переменной х2, снова возвращаемся к параметру х1 и цикл повторяется до тех пор, пока изменение любого управляемого параметра на величину выбранного шага будет приводить к увеличению значения целевой функ-

ции. Поиск заканчивается достижением локального минимума целевой функции, соответствующего значениям вектора управляемых параметров X*.

Использование метода свертки можно проиллюстрировать следующим примером. Пусть имеются две целевые функции F1{x) и F2(x) одного управляемого параметра. Предположим, что для каждой из них необходимо найти минимум и значимость каждой из них с точки зрения оптимизации выходных параметров конструкции равнозначна.

В этом случае постановка задачи, в общем виде выраженной формулой (1.1), сводится к следующей:

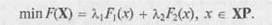
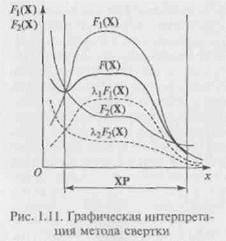
Поскольку значимость целевых функций в процессе оптимизации одинакова, весовые коэффициенты равны. Допустим, λ1 = λ2 = 0,5. Графическая интерпретация решения этой задачи представлена на рис. 1.11.

Следует иметь в виду, что на практике решение задач проектирования таких сложных объектов, как автомобиль или трактор, связано с нахождением экстремумов целевых функций значительно большего количества управляемых параметров и столь простая графическая интерпретация описанных методов невозможна.

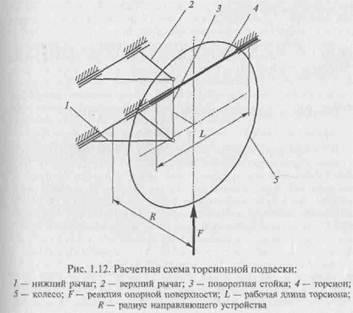
Рассмотрим пример постановки задачи оптимального проектирования независимой подвески на двух поперечных рычагах, упругим элементом которой является круглый торсион. Расчетная схема подвески приведена на рис. 1.12.

Направляющим устройством этой подвески являются нижний 1 и верхний 2 рычаги, связанные между собой поворотной стойкой 3, на которой расположена ось вращения колеса 5. С осью нижнего рычага связан торсион 4 диаметра d, расположенный вдоль оси транспортного средства. На колесо воздействует нормальная реакция опорной поверхности F, которая на радиусе направляющего устройства R создает момент, закручивающий торсион.

Потенциальная энергия деформации торсиона определяется зависимостью

Потенциальная энергия деформации торсиона определяет одну из важнейших характеристик подвески — ее энергоемкость. Чем выше энергоемкость подвески, тем менее вероятны ее пробои, что положительно сказывается как на комфортабельности автомобиля, так и на нагруженности элементов подвески и несущего основания автомобиля. Однако условия максимальной энергоемкости подвески недостаточны для того, чтобы обеспечить ее основное назначение — плавность хода автомобиля, которая оценивается частотой собственных колебаний неподрессоренной массы автомобиля на подвеске. При известной неподрессоренной массе автомобиля и радиусе R для определения частоты собственных колебаний на торсионной подвеске достаточно знать жесткость торсиона. Кроме того, необходимым условием работоспособности

подвески является прочность ее элементов, в данном случае — торсиона.

Таким образом, задачу оптимального проектирования подвески (см. рис. 1.12) можно сформулировать следующим образом.

За целевую функцию принимаем потенциальную энергию деформации торсиона, определяющую энергоемкость подвески, причем ищем максимум целевой функции.

Данные ограничения могут быть заданы проектировщиком исходя из опыта предшествующих разработок и из конструктивных особенностей проектируемого автомобиля.

Указанная задача может быть решена методами нелинейного программирования, поскольку целевая функция и ряд ограничений выражены нелинейными зависимостями.

Дата добавления: 2014-01-03