Алгоритмы логического вывода в условиях определенности

Механизм применения правила называется механизмом вывода. Существует два вида механизмов логического вывода: механизм, основанный на модели системы продукций, и механизм, основанный на модели логического программирования. Они реализуют два основных аспекта логического вывода:

нахождение всех возможных заключений из фактов и правил;

изучение предпосылок заключений с целью определения их истинности.

Таким образом, имеются два основных направления логического вывода: прямой - переход от заданных фактов к их следствиям и далее по дереву продукций, и обратный - рекуррентный поиск фактов, определяющих истинность заданного заключения.

3.2.4.1. Алгоритм прямого вывода

Реальные базы знаний часто содержат только выражения в ограниченной форме, называемые хорновскими выражениями. Хорновское выражение представляет собой дизъюнкцию литер, среди которых положительным является не больше чем одна.

Например, выражение: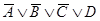

Более естественной для понимания является следующая форма выражения выше: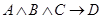

Такие выражения называются определенными. Здесь левая часть выражения (правила) называется телом выражения, а заключительная часть – головой выражения. Тело выражения состоит из предпосылок.

Хорновский дизъюнкт, состоящий из одной положительной литеры называют фактом.

Дизъюнкт без положительных литер можно записать как импликацию, у которой в заключительной части false:

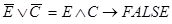
В базах данных такое выражение является ограничением целостности.

Пусть имеется БЗ, которая содержит только определенные выражения и не содержит ограничений целостности. Такие базы знаний мы будем называть находящимися в хорновской форме.

Получение логических следствий с помощью хорновских выражений может осуществляться за время, линейно зависящее от размера базы знаний.

Функция bool Fwd (kb, liter) осуществляет логический вывод об истинности входной литеры liter в базе знаний kb в хорновской форме.

Используются следующие обозначения:

agenda – “повестка дня” – список литер, о которых известно, что они истинны (в начале работы это список фактов), но еще не обработаны

count – массив, в начале работы содержащий количество предпосылок в соответствующих правилах из БЗ (т.е. размер массива равен количеству правил БЗ)

Inferred – булевый список, индексированный по литерам (содержит все литеры, которые есть в БЗ), где в начале все значения равны false.

Псевдо-алгоритм прямого логического вывода в хорновской БЗ:

bool Fwd (kb, liter)

{

while список agenda не пуст do

{

P = Pop (agenda) // извлекаем первую истинную литеру

if (!inferred[P]) do // если мы ее не обрабатывали

{

inferred[P] = true // установим, что она обработана

for each хорновское выражение C в котором присутствует

предпосылка P do

{

count[с]--; // декремент недоказанных предпосылок для С

if count[с] = 0 then do // если все предпосылки доказаны

{ // Head[c] – возвращает “голову” выражения

if Head[с] = liter then

return true // если голова выражения – liter, то ее истинность доказана

Push(Head[c], agenda) // Иначе помещаем ее в список доказанных

}

}

}

}

return false // здесь можно оказаться только в случае перебора всех вариантов и при этом истинность liter не доказана

}

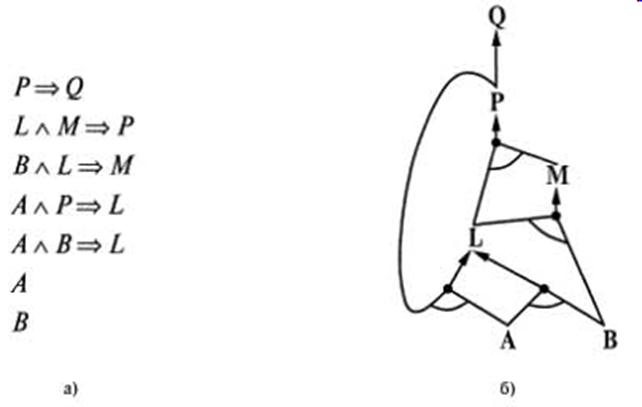
Пример применения алгоритма прямого логического вывода: простая база знаний, состоящая из хорновских выражений (а); соответствующий граф AND-OR (б)

Дуги, соединенные кривой линией, обозначают конъюнкцию (в них необходимо доказать истинность каждой дуги), а дуги, не соединенные друг с другом, обозначают дизъюнкцию.

Можно легко убедиться в том, что алгоритм прямого логического вывода является непротиворечивым: каждый этап логического вывода по сути представляет собой применение правила отделения. Кроме того, алгоритм прямого логического вывода является полным: в нем может быть получено каждое атомарное высказывание, которое следует из базы знаний. Проще всего в этом можно убедиться, рассмотрев заключительное состояние таблицы inferred (после того, как этот алгоритм достигает фиксированной точки, в которой становятся невозможными какие-либо новые этапы логического вывода).

Эта таблица содержит значение true для каждого символа, выведенного логическим путем в течение этого процесса, и false— для всех других символов. Эта таблица может рассматриваться как логическая модель; более того, ^ каждое определенное выражение в первоначальной базе знаний KB является истинным в данной модели.

Недостатки:

•В ходе работы получается множество ненужных выводов

•Низкая эффективность

•Не используется в ходе естественных человеческих рассуждений из-за крайней избыточности

3.2.4.2. Алгоритм обратного вывода

Алгоритм обратного логического вывода, как указывает само его название, действует в обратном направлении от запроса. Если удается сразу же узнать, что высказывание, содержащееся в запросе Liter, является истинным, то не нужно выполнять никакой работы. В противном случае алгоритм находит те импликации в базе знаний, из которых следует Liter Если можно доказать, что все предпосылки одной из этих импликаций являются истинными (с помощью обратного логического вывода), то высказывание Liter также является истинным. Будучи применен к запросу Q, показанному на рисунке, этот алгоритм будет проходить вниз по графу до тех пор, пока не достигнет множества известных фактов, которые образуют основу для доказательства.

Обратный логический вывод представляет собой одну из форм рассуждения, направляемого целями. Такая форма является полезной при получении ответов на конкретные вопросы, наподобие следующих: "Что теперь мне следует делать?" и "Где же находятся мои ключи?" Зачастую стоимость обратного логического вывода намного меньше по сравнению со стоимостью, линейно зависящей от размера базы знаний, поскольку в этом процессе затрагиваются только факты, непосредственно относящиеся к делу.

Словесный алгоритм обратного вывода:

Bool Back (kb, liter)

•Поиск искомой литеры в фактах. Если литера есть, то ее истинность известна. Выход.

•Анализируем i-ое высказывание. Если в заключительной части высказывания присутствует liter, то формируем результат как: res = Back(kb, A) && Back(kb, B) && Back(kb, C)…

•возвращаем res, если оно истинно.

•Если не конец БЗ, то i++ и переходим к 2.

•Иначе возвращаем false

Алгоритм обратного вывода, как видно, является рекурсивным, поэтому необходимо избегать зацикливания из-за выражений типа A->B и B->A.

На обратном выводе построен механизм, реализованный в Прологе. Обратный вывод применяется при диагностике и классификации.

Механизм обратного вывода был разработан позже, чем механизм прямого вывода. Он считается более гибким, устойчивым и значительно эффективнее по временным показателям.

Дата добавления: 2014-01-03