Механический смысл определенного интеграла

Тема: Механические и геометрические смыслы определенного интеграла. Необходимое условие интегрируемости

Лекция 9

Пусть материальная точка М перемещается под действием силы 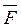, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х – абсцисса движущейся точки М.

Найдем работу А силы 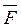по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (a<b). Для этого отрезок [a; b] точками а = х₀, х₁,..., b = х_n (х₀< х₁<...< х_n) разобьем на n частичных отрезков [х₀; х₁], [х₁; х₂],..., [х_n-1; х_n]. Сила, действующая на отрезке [х_i-1; х_i], меняется от точки к точке. Но если длина отрезка Δх_i = х_i – х_i-1 достаточно мала, то сила 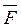на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = c_i 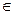[х_i-1; х_i]. Поэтому работа, совершенная этой силой на отрезке [х_i-1; х_i], равна произведению F(c_i)∙Δх_i. Приближенное значение работы А силы 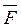на всем отрезке [a; b] есть

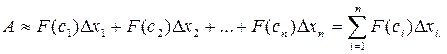
Это приближенное равенство тем точнее, чем меньше длина Δх_i. Поэтому за точное значение работы А принимается предел суммы при условии, что наибольшая длина λ частичных отрезков стремится к нулю:

.

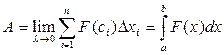Итак, работа переменной силы 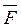, величина которой есть непрерывная функция F = F(x), действующая на отрезке [a; b], равна определенному интегралу от величины F(x) силы, взятому по отрезу [a; b].

В этом состоит механический смысл определенного интеграла.

Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от t = a до t = b, равен определенному интегралу от скорости v(t):

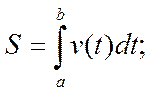
масса т неоднородного стержня на отрезке [a; b] равна определенному интегралу от плотности

γ(х):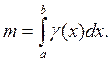

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

Если f (x) непрерывна и положительна на [ a, b ], то интеграл

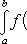
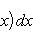
представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x) (см. рис. 5.).

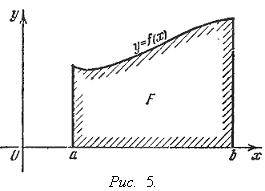
Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f (x), заданная на промежутке [ a, b ], равна нулю во всех точках этого промежутка, кроме конечного числа точек z ₁, z ₂,..., z_N. Составим для f (x) интегральную сумму σ.

Пусть из точек ξ ₀, ξ ₁,..., ξ_{n -1}, входящих в определение σ, p точек совпадают с точками z_i, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f (z_i) | (i = 1, 2,..., N) есть K, то, очевидно,

| σ | ≤ Kpλ ≤ KNλ,

откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл

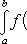
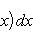
существует и равен нулю.

Приведем теперь пример функции, не имеющей интеграла. Пусть φ (x) задана на промежутке [0, 1] так:

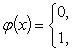
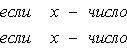
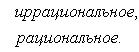
Если мы, составляя сумму σ, за точки ξ_k выберем числа иррациональные, то окажется σ = 0. Если же все ξ_k взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл

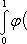
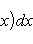
не существует.

В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций.

Дата добавления: 2014-01-03