Преобразование значений

Иногда возникает необходимость сопоставить между собой результаты диагностики, полученной с помощью разных тестов и, соответственно, представленной в разнобальных шкалах. Например, 65 баллов по шкале «личностная тревожность» (опросник Спилбергера) и 65 баллов по шкале «общий интеллект» (тест Амтхауэра). Много это или мало? Такой балл означает очень высокую личностную тревожность и пониженный интеллект (интеллектуальную недостаточность).

Существуют разные способы для того, чтобы перевести результаты диагностики в одну шкалу. Один из таких методов предложен О.П.Елисеевым[10] - шкала 20 - 80. Для перехода к этой шкале каждое значение по всем тестам необходимо преобразовать по формуле:

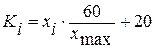, где

x_i - значение испытуемого по тесту или шкале,

x_max - максимальное количество баллов, которое может получить индивид по этому тесту или шкале.

Покажу на примере. В результате психодиагностики уровня интеллекта и нейротизма мы получили данные, которые преобразуем в шкалу 20 - 80. Максимальное значение по шкале интеллекта - 130, по шкале нейротизма - 20. Тогда у первого испытуемого:

интеллект 101; 101 × 60 / 130 + 20 = 66,7

нейротизм 15; 15 × 60 / 20 + 20 = 65,0.

Действуя таким же образом, преобразуем все остальные показатели (табл. 5).

Таблица 5.

Перевод баллов в шкалу 20 - 80

Испытуемые	Сырые баллы	Шкала 20 - 80
интеллект	нейротизм	интеллект	нейротизм
			66,7	65,0
			45,7	56,0
			44,8	50,0
			71,2	71,0
			66,2	71,0
			66,2	71,0
			64,3	62,0
			65,2	59,0
			73,1	80,0
			63,8	50,0

Обратите внимание, цифры получились одного порядка, их можно представить на одном графике, одной гистограмме.

Другой часто используемый способ преобразования показателей - использование шкалы стенов или «стандартной десятки». Его можно использовать там, где не определен максимально возможный уровень показателей, но выборка (т.е. группа испытуемых) должна быть при этом достаточно большой (чем больше, тем лучше, но не меньше 30 человек). Считается, что в большой выборке результаты по любому показателю распределены нормально, т.е. низких и высоких показателей мало, а средних - много. Это можно представить кривой, которая известна как кривая Гаусса (см. рис.11.)

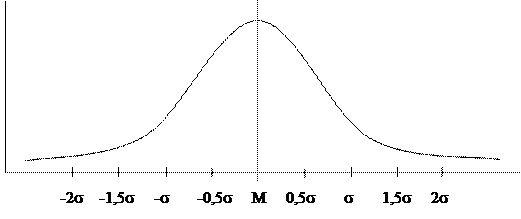
Рис. 11. Кривая нормального распределения Гаусса

Например, если сравнить всех людей по росту, то низких и высоких людей - мало, в основном люди среднего роста. Весь диапазон возможных результатов делится на 10 частей, каждая из которых равна 0,5s. s - это статистический показатель, называемый «стандартное отклонение», или «среднее квадратичное отклонение», или «дисперсия». Не будем здесь вдаваться в подробности (см. пункт «Оценка типа распределения первичных результатов»), укажу только алгоритм перевода.

Необходимо вычислить два статистических показателя:

- среднее арифметическое 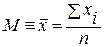, т.е. сумма всех показателей делится на количество испытуемых (М и 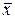- равнопринятые обозначения средней арифметической,

- стандартное отклонени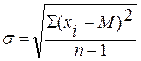е , где

x_i – каждое из значений, М – среднее арифметическое значение,

n – количество значений

Покажу на том же примере (про интеллект и нейротизм), хотя это и не корректно, т.к. мало испытуемых. Построим вспомогательную таблица для расчетов.

Таблица 6.

Вспомогательная таблица для расчета стандартного отклонения

№ п/п	Интеллект xi	xi - M	(xi - M)^2		№ п/п	Нейротизм xi	xi - M	(xi - M)^2
		-0,2	0,04			0,5	0,25
		-2,2	4,84			-2,5	6,25
		-4,2	17,64			-4,5	20,25
		9,8	96,04			2,5	6,25
		-1,2	1,44			2,5	6,25
		-1,2	1,44			2,5	6,25
		-5,2	27,04			-0,5	0,25
		-3,2	10,24			-1,6	2,25
		13,8	190,44			5,5	30,25
		-6,2	38,44			-4,5	20,25
								S(xi - M)^2= = 98,5

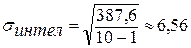
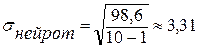
Теперь определяем точные границы интервалов.

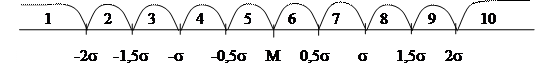Переводим шкалу интеллекта в стены:

М = 101,2 - это граница между 5 и 6 стенами.

101,2 + 0,5 × 6,56 = 104,5 - граница между 6 и 7 стенами,

101,2 - 0,5 × 6,56 = 97,92 - граница между 4 5 стенами.

И так далее.

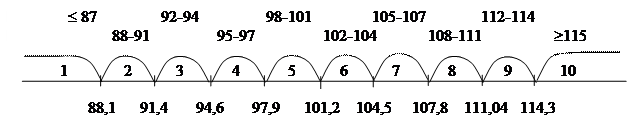
Аналогично в стены переводятся показатели нейротизма:

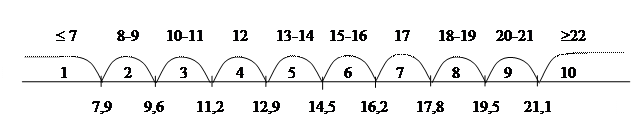
Сведем все данные в таблицу.

Таблица 7.

Преобразование показателей в шкалу 20 - 80 и шкалу стенов

Испытуемые	Сырые баллы	Шкала 20 - 80	Шкала стенов
интеллект	нейротизм	интеллект	нейротизм	интеллект	нейротизм
			66,7	65,0
			45,7	56,0
			44,8	50,0
			71,2	71,0
			66,2	71,0
			66,2	71,0
			64,3	62,0
			65,2	59,0
			73,1	80,0
			63,8	50,0

Совсем не обязательно использовать оба способа. Выберите, что Вам больше нравится. Теперь эти данные можно представить на одном графике, на одной гистограмме.

Группировка результатов в классовые интервалы

При большом массиве данных все значения группируются в классовые интервалы и уже затем могут быть представлены в виде полигона распределения частот.

Интервалы формируются по определенному алгоритму[11]:

- находят максимальный (x_max) и минимальный (x_min) показатели,

- определяют размах распределения (x_max - x_min),

- выбирают величину классового интервала; в качестве величин, характеризующих ширину класса группировки, используют следующие шаги: 1, 2, 3, 5, 10, 20 и т.д.

- общее количество интервалов чаще всего не менее 8 и не более 20,

- точно обозначают границы интервалов,

- классу, содержащему минимальные величины первичных сырых баллов, присваивают номер 1, далее по возрастающей.

Рассмотрим на примере.

В результате диагностики умения читать вслух учащиеся 3^х классов получили следующие данные (количество прочитанных без ошибок слов за 1 мин):

78, 48, 59, 77, 78, 71, 66, 90, 60, 108, 70, 69, 76, 72, 85, 83, 81, 112, 57, 60, 59, 57, 99, 59, 70, 87, 87, 73, 72, 70, 79, 80, 58, 57, 67, 53, 51, 50, 70.

Найдем максимальное и минимальное значения: x_max = 112, x_min = 48.

Размах распределения 112 - 48 = 64.

Выберем величину классового интервала.

Если взять 2: 64 / 2 = 32 класса - слишком много классов, мелкий шаг.

Если взять 5: 64 / 5» 13 классов.

Построим таблицу.

Таблица 8.

Группировка первичных результатов исследования умения читать вслух

класс	границы	точные границы	центр класса	первичное распределение	частота
	108 – 112	107,5-112,5		ХХ
	103 – 107	102,5-107,5
	98 – 102	97,5-102,5		X
	93 – 97	92,5-97,5
	88 – 92	87,5-92,5		X
	83 – 87	82,5-87,5		XXXX
	78 – 82	77,5-82,5		XXXXX
	73 – 77	72,5-77,5		XXX
	68 – 72	67,5-72,5		XXXXXXXX
	63 – 67	62,5-67,5		X
	58 – 62	57,5-62,5		XXXXXXX
	53 – 57	52,5-57,5		XXXX
	48 - 52	47,5-52,5		XXX
					Sf = 39

При построении полигона частот для структурированных таким образом данных на оси абсцисс (ось Х) отмечают номера классов, а на оси ординат (ось У) – отдельные частоты.

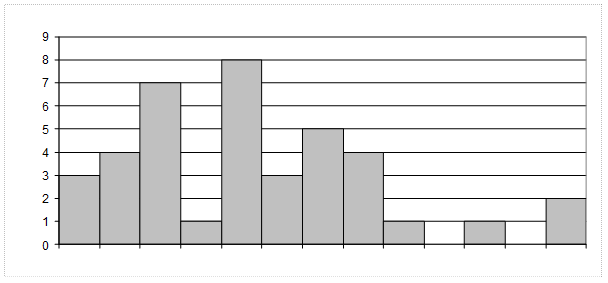Рис. 12. Гистограмма и полигон частот

Обратите внимание, некоторые классы оказались «пустыми». Такое случается, когда мы берем равные интервалы. Чуть далее я покажу Вам еще один способ разбиения на классовые интервалы, где интервалы не равны друг другу.

Дата добавления: 2014-01-03