АЛГОРИТМ. Это очень простой критерий, который позволяет быстро оценить различия между двумя выборками

Q – критерий Розенбаума

Это очень простой критерий, который позволяет быстро оценить различия между двумя выборками. Однако если критерий Q не выявляет достоверных различий, это еще не означает, что их действительно нет.

Статистические гипотезы:

Но: уровень признака в выборке 1 не превышает уровня признака в выборке 2.

Н1: уровень признака в выборке 1 превышает уровень признака в выборке 2.

подсчета критерия Q Розенбаума [14]

1. Проверить, выполняются ли ограничения критерия: n₁,n₂≥ 11, n₁».n2

2. Упорядочить значения отдельно в каждой выборке по степени воз­растания признака. Считать выборкой 1 ту выборку, значения в которой предположительно выше, а выборкой 2 - ту, где значения предположительно ниже.

3. Определить самое высокое (максимальное) значение в выборке 2.

4. Подсчитать количество значений в выборке 1, которые выше максимального значения в выборке 2. Обозначить полученную величину как S₁.

5. Определить самое низкое (минимальное) значение в выборке 1.

6. Подсчитать количество значений в выборке 2, которые ниже мини­мального значения выборки 1. Обозначить полученную величину как S_2.

7. Подсчитать эмпирическое значение Q по формуле: Q=S₁+S₂.

8. По Табл. 2 Приложения 3 определить критические значения Q для данных n₁ и n2. Если Q_эмп равно Q_0,05 или превышает его, Н₀ от­вергается.

9. При n₁,n2 >26 сопоставить полученное эмпирическое значение с Q_кр=8 (р ≤0,05) и Q_кр=10 (p ≤0,01). Если Q_эмп превышает или по крайней мере равняется Q_кр=8, H₀ отвергается.

Пример

В результате диагностики уровня тревожности у 16 девочек и 14 мальчиков 1а класса получены следующие данные (табл. 12.1). Можно ли утверждать, что у девочек и мальчиков разный уровень тревожности (показатели тревожности в одной из подгрупп достоверно выше)?

Таблица 12.1

Индивидуальные значения тревожности у девочек (n=16) и мальчиков (n=14)

Девочки		Мальчики
№	Код имени	Показатели	№	Код имени	Показатели

Количество человек в группах n₁, n₂ ³ 11. Требования к критерию соблюдаются.

Упорядочим данные по убыванию в подгруппах.

Таблица 12.2

Упорядоченные данные тревожности

1 ряд – девочки	2 ряд – мальчики
		20
			9

Обратите внимание, мы правильно обозначили ряды: первый – тот, что выше – ряд девочек, второй, «ниже» - ряд мальчиков.

По таблице 12.2 определяем количество значений первого ряда, которые больше максимального значения второго ряда: S₁ = 5.

Определим количество значений второго ряда, которые меньше минимального значения первого ряда: S₂ = 6.

Вычислим Q_эмп: Q_эмп = S₁ + S₂ = 5+6=11.

По Табл. 2 Приложения 3 определяем критические значения Q для n₁=16, n₂=14.

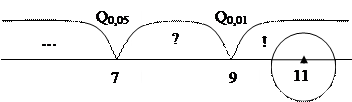
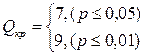Построим ось значимости.

Q_эмп > Q_кр (р ≤0,01)

Ответ: Н₀ отклоняется, принимается Н₁: у девочек данного класса уровень тревожности достоверно выше.

Если бы Q_эмп оказалось в диапазоне от 7 до 9, Н₀ также можно было бы отклонить, но уровень значимости был бы р ≤0,05 (т.е. вероятность ошибки выше).

Дата добавления: 2014-01-03