АЛГОРИТМ. 1. Определить те значения признака, которые будут критерием для разделения испытуемых на тех, у кого «есть эффект» и тех

расчета критерия φ* [16]

1. Определить те значения признака, которые будут критерием для разделения испытуемых на тех, у кого «есть эффект» и тех, у кого «нет эффекта». Если признак измерен количественно, использовать критерий l, для поиска оптимальной точки разделения.

2. Начертить четырехклеточную таблицу из двух столбцов и двух строк. Пер­вый столбец – «есть эффект»; второй столбец – «нет эффекта»; первая строка сверху - 1 группа (выборка); вторая строка - 2 группа (выборка).

3. Подсчитать количество испытуемых в первой группе, у которых «есть эффект» и занести это число в левую верхнюю ячейку таблицы.

4. Подсчитать количество испытуемых в первой выборке, у которых «нет эф­фекта», и занести это число в правую верхнюю ячейку таблицы. Подсчитать сумму по двум верхним ячейкам. Она должна совпадать с количеством ис­пытуемых в первой группе.

5. Подсчитать количество испытуемых во второй группе, у которых «есть эф­фект», и занести это число в левую нижнюю ячейку таблицы.

6. Подсчитать количество испытуемых во второй выборке, у которых «нет эф­фекта», и занести это число в правую нижнюю ячейку таблицы. Подсчитать сумму по двум нижним ячейкам. Она должна совпадать с количеством испытуемых во второй группе (выборке).

7. Определить процентные доли испытуемых, у которых «есть эффект», путем отнесения их количества к общему количеству испытуемых в данной группе (выборке). Записать полученные процентные доли соответственно в левой верхней и левой нижней ячейках таблицы в скобках, чтобы не перепутать их с абсолютными значениями.

8. Проверить, не равняется ли одна из сопоставляемых процентных долей ну­лю. Если это так, попробовать изменить это, сдвинув точку разделения групп в ту или иную сторону. Если это невозможно или нежелательно, от­казаться от критерия φ* и использовать критерий c².

9. Определить по Табл. 4 Приложения 3 величины углов φ для каждой из
сопоставляемых процентных долей.

10. Подсчитать эмпирическое значение φ* по формуле:

,

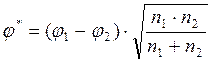где: φ₁ - угол, соответствующий большей процентной доле,

φ₂ – угол, соответствующий меньшей процентной доле,

n₁ – количество наблюдений в выборке 1,

n₂ – количество наблюдений в выборке 2.

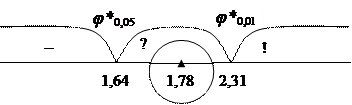
11. Сопоставить полученное значение φ* с критическими значениями:
φ*≤1,64 (р≤0,05) и φ*≤2,31 (р≤0,01). Если φ^*_эмп≥φ^*_кр, Н₀ отвергается.

Пример 1: сопоставление выборок по качественно определяемому признаку.

После проведения формирующего эксперимента учащимся 5 а (экспериментальная группа) и 5 б (контрольная группа) по трем не связанным друг с другом словам написать мини-сочинение. В 5а (ЭГ) из 25 человек с задачей справились 18 человек, в 5 б (КГ) из 27 человек с задачей справились 16 человек. достоверны ли различия между группами?

Выполним первые 8 шагов алгоритма и составим четырехклеточную таблицу.

Таблица 14.

Группы	«есть эффект», задание выполнено	«нет эффекта», задание не выполнено	Суммы
Кол-во	% доля	Кол-во	% доля
5 а		(72 %)		(28 %)
5 б		(48,1 %)		(51,9 %)
Суммы

Шаг 9. Определим по Таблице 4 приложения 3 величины φ:

φ_{1(72 %)} = 2,026; φ_{2(48,1 %)} =1,533

Шаг 10. Подсчитаем эмпирическое значение φ* по формуле:

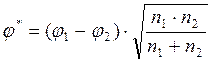
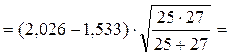
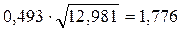
Шаг 11. Сопоставим φ*_эмп с критическим значением.

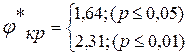
φ*_{эмп >} φ*_{кр 0,05.}

Ответ: Н₀ отвергается. Доля учащихся, справившихся с заданием, в экспериментальной группе больше, чем в контрольной (р ≤0,05).

Пример 2 - сопоставление двух выборок по количественно измеряемому признаку

При проведении диагностики экстраверсии и нейротизма с использованием опросника Айзенка в двух студенческих группах (n₁ =29, n₂ =31) по шкале лжи получены баллы от 0 до 8. Известно, что при показателях больше 4 баллов по этой шкале ответы испытуемых считаются недостоверными. В первой группе 9 человек получили по шкале лжи больше 4 баллов, во второй группе – 7 человек. Можно ли считать, что различия между группами по уровню лжи достоверны?

Граница, по которой мы делим выборку на части «есть эффект – нет эффекта» задана самим опросником – 4 балла.

Далее следуем по алгоритму. Занесем данные в таблицу. Обозначим группой 1 ту, в которой больше людей, у которых «есть эффект».

Таблица 15.

Группы	«есть эффект», Ложь > 4	«нет эффекта», Ложь ≤ 4	Суммы
Кол-во	% доля	Кол-во	% доля
Группа 1		(31%)		(69 %)
Группа 2		(22,6 %)		(77,4 %)
Суммы

Шаг 9. Определим по Таблице 4 приложения 3 величины φ:

φ_1(31%) = 1,182; φ_{2(22,6 %)} =0,991

Шаг 10. Подсчитаем эмпирическое значение φ* по формуле:

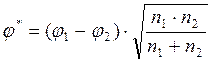
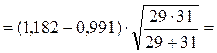
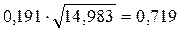
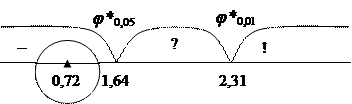Шаг 11. Сопоставим φ*_эмп с критическим значением.

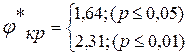
Ответ: Н₀ принимается. Доля лиц, имеющих повышенные показатели по шкале лжи в первой группе, не выше такой же доли во второй группе. Другими словами, различий между группами по этому показателю нет!

Дата добавления: 2014-01-03