Алгоритм

U – критерий Манна – Уитни

Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявить различия между малыми выборками, когда n₁, n₂ ≥ 3 или n₁= 2, n₂≥ 5 и является более мощным, чем критерий Q Розенбаума.

Гипотезы:

Н₀: Уровень признака в группе 2 не ниже уровня признака в группе 1.

Н₁: Уровень признака в группе 2 ниже уровня признака в группе 1.

подсчета критерия U Манна-Уитни [15]

1. Перенести все данные испытуемых на индивидуальные карточки.

2. Пометить карточки испытуемых выборки 1 одним цветом, скажем красным, а все карточки из выборки 2 - другим, например синим.

3. Разложить все карточки в единый ряд по степени нарастания при­знака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой.

4. Проранжировать значения на карточках, приписывая меньшему зна­чению меньший ранг, а одинаковым значениям – ранг, являющийся средним арифметическим значением от вероятных рангов (см. стр. 28). Всего рангов получится столько, сколько у нас (n₁+п₂).

5. Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие - в другой.

6. Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли об­щая сумма рангов с расчетной, которая вычисляется по формуле .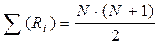

7. Определить большую из двух ранговых сумм.

8. Определить значение U по формуле:

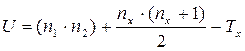, где

n₁ - количество испытуемых в выборке 1;

n₂ - количество испытуемых в выборке 2;

Т_х - большая из двух ранговых сумм;

n_х - количество испытуемых в группе с большей суммой рангов.

9. Определить критические значения U по Табл. 3 Приложения 3. Если U_эмп>U_кр0,05, Н₀ принимается. Если U_эмп≤U_кр0,05, Н₀ от­вергается. Чем меньше значения U, тем достоверность различий выше.

Пример.

В НПК № 3 у студентов-филологов и студентов специальности «учитель начальных классов» диагностировали уровень интеллекта. Результаты представлены в табл. 13.1. можно ли сказать, что студенты разных специальностей обладают разным уровнем интеллекта.

Таблица 13.1.

Индивидуальные значения уровня интеллекта в выборке студентов специальности «учитель начальных классов» (n₁=14) и студентов-филологов (n₂=12)

Студенты «началка»	Студенты-филологи
И.А. К.А. К.Е. П.А. С.А. Ст.А. Т.А. Ф.А. Ч.И. Ц.А. См.А. К.Ан. Б.Л. 14. Ф.В		Н.Т. О.В. Е.В. Ф.О. И.Н. И.Ч. И.В. К.О. P.P. Р.И. O.K. 12. Н.К.

Данный метод основан на подсчете рангов.

Запомните правила ранжирования. Их три:

1. Меньшему значению начисляется меньший ранг.

2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.

3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле 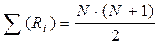, где N – общее количество ранжируемых наблюдений.

В нашем примере, проделав шаги 1 – 6 алгоритма, получим следующие данные.

Таблица 13.2.

Подсчет ранговых сумм

Студенты-«началка» (n1=14)	Студенты -филологи (п2=12)
Показатель интеллекта	Ранг	Показатель интеллекта	Ранг
	20,5
	20,5
	15,5		15,5
	11,5		11,5
	11,5
	11,5
	6,5		6,5
	4,5		4,5
Суммы
Средние	107,2		111,5

Общая сумма рангов 165 + 186 = 351.

Расчетная сумма: 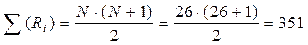. Ошибки нет.

Шаг 7. Бόльшая сумма рангов – в группе студентов – филологов (Т_х=186).

Шаг 8. Определим значение U.

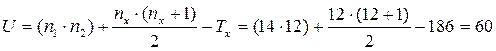
Шаг 9. Определим критические значения U по Табл.3 Прил. 3 для n₁ =14 и n₂ =12.

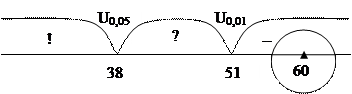
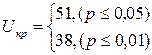
U_эмп > U_кр.

Ответ: Н₀ принимается. Группа студентов-филологов не превосходит группу студентов «началки» по уровню интеллекта, т.е. различия недостоверны.

φ^*-критерий (угловое преобразование Фишера)

Данный критерий относится к группе многофункциональных. Это означает, что он может использоваться по отношению к самым разнообразным данным, выборкам и задачам. Выборки могут быть разными, а можно сопоставлять данные, полученные на одной выборке в разных условиях.

Многофункциональный критерий построен на сопоставлении долей, выраженных в долях единицы или в процентах. Суть критерия состоит в определении того, какая доля наблюдений (реакций, выборов, испытуемых) в данной выборке характеризуется интересующим нас эффектом. Таким эффектом может быть:

- определенное значение качественно определяемого признака (например, отнесенность к определенному полу, выражение согласия с каким-либо предложением и др.),

- определенный уровень количественно измеряемого признака (например, получение оценки, превосходящей проходной бал; выбор дистанции в разговоре, превышающей 50 см и др.),

- определенное соотношение значений или уровней исследуемого признака (например, преобладание положительных сдвигов над отрицательными; преимущественное проявление крайних значений признака).

Другими словами, здесь сводятся любые данные к альтернативной шкале «есть эффект – нет эффекта». Важно, что ни одна из сопоставляемых долей не должна быть равной нулю!!!

Гипотезы:

Н₀: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.

Н₁: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.

Дата добавления: 2014-01-03