АЛГОРИТМ. расчета критерия l при сопоставлении двух эмпирических распределений[19]

расчета критерия l при сопоставлении двух эмпирических распределений [19]

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты, полученные в распределении 1 (первый столбец) и в распределении 2 (второй столбец).

2. Подсчитать эмпирические частости по каждому разряду для распределения 1 по формуле:

f_эмп - эмпирическая частота в данном разряде, n₁ - количество наблюдений в выборке.  

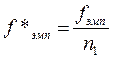, где

Занести эмпирические частости распределения 1 в третий столбец.

3.

f_эмп - эмпирическая частота в данном разряде, n₂ - количество наблюдений во 2 выборке.  

Подсчитать эмпирические частости по каждому разряду для распределения 2 по формуле:

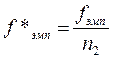, где

Занести эмпирические частости распределения 2 в четвертый столбец таблицы.

4. Подсчитать накопленные эмпирические частости для распределения 1 по форму­ле:

,

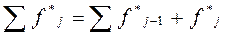где Σf^*_j - частость, накопленная на предыдущих разрядах;

j - порядковый номер разряда;

f^*_j - эмпирическая частость данного j-го разряда.

Полученные результаты записать в пятый столбец.

5. Подсчитать накопленные эмпирические частости для распределения 2 по той же формуле и записать результат в шестой столбец.

6. Подсчитать разности между накопленными частостями по каждому разряду. Записать в седьмой столбец абсолютные величины разностей, без их знака. Обозначить их как d.

7. Определить по седьмому столбцу наибольшую абсолютную величину разности d_max.

8.

n₁ - количество наблюдений в 1 выборке, n₂ - количество наблюдений во 2 выборке.  

Подсчитать значение критерия l по формуле:

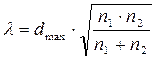, где

9. По Табл. 9 Приложения 3 определить, какому уровню статистической зна­чимости соответствует полученное значение l.

Если l_эмп≥1,36, различия между распределениями достоверны.

Таблица 22.3.

	пн	вт	ср	чт	пт	Сумма
Работоспособность

Построим вспомогательную таблицу для расчетов и будем действовать по алгоритму.

Таблица 22.4.

Вспомогательная таблица расчета l - критерия

	Эмпирические частоты	Эмпирические частости	Накопленные эмпирические частости	Разность
	f1	f2	f*1	f*2	Σf*1	Σf*2	Σf*1 - Σf*2
Пн			0,247	0,241	0,247	0,241	0,006
Вт			0,296	0,276	0,543	0,516	0,027
Ср			0,235	0,218	0,778	0,735	0,043
Чт			0,099	0,104	0,877	0,839	0,038
Пт			0,123	0,161	1,000	1,000	0,000
Сумма			1,000	1,000

Шаг1. Перенесем из таблиц 22.1. и 22.3 эмпирические частоты в распределении работоспособности по дням недели f₁ и f_{2 .}

Шаг 2-3. Подсчитаем эмпирические частости по каждому разряду и каждому распределению.

Шаг 4-5. Подсчитаем накопленные эмпирические частости по каждому из распределений.

Шаг 6-7. Подсчитаем разности и определим d_max. В нашем случае d_max= 0,043.

Шаг 8. Рассчитаем значение критерия l.

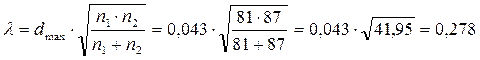
Шаг 9. По таблице 9 Приложения 3 определим уровень статистической значимости. р = 0,99. В психологии в качестве уровней значимости рассматриваются обычно р ≤0,005 и р ≤0,001.

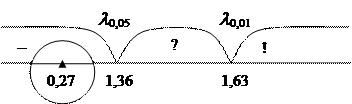Построим для наглядности ось значимости.

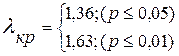
Критические значения l не зависят от величины выборки, поэтому их можно просто запомнить.

Ответ: Н₀ принимается. Распределения, полученные в исследованиях двух студенток, не отличаются друг от друга.

Дата добавления: 2014-01-03