АЛГОРИТМ. расчета коэффициента ранговой корреляции Спирмена rs[20]

расчета коэффициента ранговой корреляции Спирмена r_s [20]

1. Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные А и В.

2. Проранжировать значения переменной А, начисляя ранг 1 наимень­шему значению, в соответствии с правилами ранжирования (см. стр.59). Занести ранги в первый столбец таблицы по порядку номе­ров испытуемых или признаков.

3. Проранжировать значения переменной В, в соответствии с теми же правилами. Занести ранги во второй столбец таблицы по порядку номеров испытуемых или признаков.

4. Подсчитать разности d между рангами А и В по каждой строке таблицы и занести в третий столбец таблицы.

5. Возвести каждую разность в квадрат: d². Эти значения занести в четвертый столбец таблицы.

6. Под считать сумму квадратов Σd².

7. При наличии одинаковых рангов рассчитать поправки:

, ,

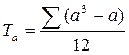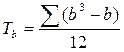где а - объем каждой группы одинаковых рангов в ранговом ряду А;

b - объем каждой группы одинаковых рангов в ранговом ряду В.

8. Рассчитать коэффициент ранговой корреляции r_s по формуле:

а) при отсутствии одинаковых рангов

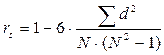
б) при наличии одинаковых рангов

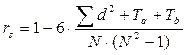
где Σd² - сумма квадратов разностей между рангами;

Т_а и T_b - поправки на одинаковые ранги;

N - количество испытуемых или признаков, участвовавших в ранжировании.

9. Определить по Табл. 10 Приложения 3 критические значения r_s для данного N. Если r_s превышает критическое значение или, по крайней мере равен ему, корреляция достоверно отличается от 0.

Пример

Для примера воспользуемся данными из Таблицы 5. определим, существует ли связь между нейротизмом и уровнем интеллекта.

Действуем по алгоритму.

Шаг 2-3. Проранжируем значения переменных.

Шаг 4. Подсчитаем разности d между рангами А и В, занесем в таблицу.

Шаг 5-6. Возведем каждую разность в квадрат и суммируем квадраты разностей.

Таблица 23

№ п/п	Аi	Bi	RA	RB	|d|	d^2
				9,5	1,5	2,25
			4,5		1,5	2,25
			4,5		1,5	2,25
				9,5	0,5	0,25
			Σ RA= 55	Σ RВ= 55		25,5

Шаг 7. У нас есть повторяющиеся ранги в переменных А и В. Рассчитаем поправки. В ряду А – одна группа одинаковых рангов – два значения, значит, а=2.

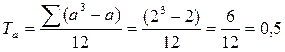
В ряду В две группы одинаковых рангов, одна в 2 значения, значит, b₁=2; вторая в 3 значения, значит b₂=3.

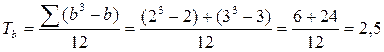
Рассчитаем коэффициент ранговой корреляции. У нас есть повторяющиеся ранги, значит, используем формулу

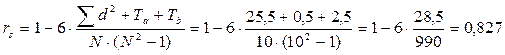
Шаг 9. Определим по Таблице 10 Приложения 3 критические значения для данного N.

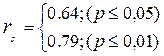
Ответ: Н₀ отвергается. Корреляция значима (р≤0,01), т.е. существует статистически достоверная связь между показателями нейротизма и интеллекта в данной группе.

Дата добавления: 2014-01-03