Расчета коэффициента линейной корреляции Пирсона

АЛГОРИТМ

Коэффициент линейной корреляции Пирсона

Данный критерий используется при сравнении интервальных величин и при условии нормального распределения признака.

1. Определите, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные Х и Y.

2. Занести во второй и третий столбцы таблицы отдельные значения X и Y, соответствующие результатам каждого индивида.

3. Вычислите средние арифметические значения для результатов X и Y по формулам

, ,

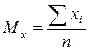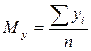где x_i – индивидуальные значения переменной x i -ого испытуемого,

y_i – индивидуальные значения переменной y i -ого испытуемого,

n – количество испытуемых.

4. Определите отклонение каждого результата переменной X от средней арифметической: 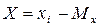. Результат запишите в четвертый столбец таблицы. Проверьте полученные результаты на наличие ошибок. Сумма X должна быть равна нулю.

5. Определите отклонение каждого результата переменной Y от средней арифметической: 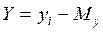. Результат запишите в пятый столбец таблицы. Проверьте полученные результаты на наличие ошибок. Сумма Y должна быть равна нулю.

6. Возведите в квадрат значения каждого значения каждого отклонения X и Y. Результаты запишите в шестой и седьмой столбцы таблицы соответственно.

7. Сложите квадраты отклонений для получения ΣX² и ΣY². Вычислите стандартные отклонения.

, ,

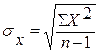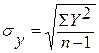где X – отклонение первичного результата x_i от средней арифметической M_x,

Y – отклонение первичного результата y_i от средней арифметической M_y /

8. Вычислите произведение отклонений X и Y. Записать результат в восьмой столбец.

9. Суммируйте все отдельные XY, учитывая соответствующие им знаки плюсы или минусы.

10. Вычислите коэффициент корреляции по формуле[21]:

.

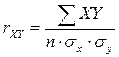11. Определите по таблице 11 Приложения 3 критические значения r_XY для данного n. Если r_XY превышает критические значения или, по крайней мере, равны ему, корреляция достоверно отличается от нуля.

Пример. У нас есть два ряда значений (табл. 24). Вычислим коэффициент корреляции. Действуем по алгоритму.

Таблица 24.

Вспомогательная таблица для расчета

	xi	yi	X (xi-Mx)	Y (yi-My)	X^2	Y^2	XY
			-4	-2,8		7,84	11,2
			-2	-1,8		3,24	3,6
				3,2		10,24	6,4
				6,2		38,44	37,2
			-1	-1,8		3,24	1,8
				-1,8		3,24	-1,8
				9,2		84,64	64,4
			-2	-2,8		7,84	5,6
			-3	-3,8		14,44	11,4
			-4	-3,8		14,44	15,2
Σ	90	158	0	0	140	187,6	155
М	9	15,8

Шаг 7. Вычислим суммы квадратов отклонений, чтобы вычислить стандартные отклонения.

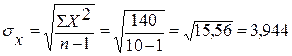
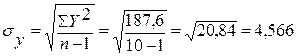
Шаг 10. Подсчитаем коэффициент корреляции.

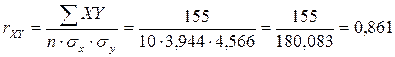
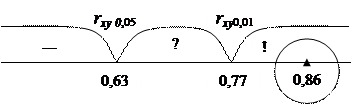Шаг 11. Найдем критические значения по таблице.

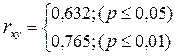
Ответ: Между данными рядами значений существует значимая корреляционная связь (p≤0,01).

Дата добавления: 2014-01-03