Специфика временных рядов как источника данных в эконометрическом моделировании

Аналитическое выравнивание временных рядов.

Специфика временных рядов как источника данных в эконометрическом моделировании.

Тема № 6. Характеристики временных рядов

Эконометрическую модель можно построить, используя два типа исходных данных:
данные, характеризующие совокупность различных объектов в определенный момент (период) времени;
данные, характеризующие один объект за ряд последовательных моментов (периодов) времени.
Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные по данным второго типа, назыв. моделями врем. рядов.
Врем. ряды являются осн. источником инфы в эконометрике. Модели на основе рядов динамики могут строиться по 2м направлениям:
По изолированному динамическому ряду
На основе системы рядов динамики, когда один ряд рассматривается как моделируемый объект, а другие – как его факторы.
Временной ряд — это совокупность значений какого-либо показателя за несколько последовательных моментов (периодов) времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:
- факторы, формир. тенденцию ряда (T);
- факторы, формир. циклические колебания ряда (P);
- случ. факторы (E).
Т.о. уровень динам. ряда можно рассматривать как ф-ю: yt = f (T, P, E)
При разл. сочетаниях этих факторов зависимость уровней ряда от времени может принимать разные формы.
Во-первых, большинство временных рядов экономических показателей имеют тенденцию, хар-ую совокупное долговрем. воздействие множества факторов на динамику изучаемого показателя. По всей видимости, эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию. На рис. 6.1 а, б, в показаны компоненты гипотетического временного ряда, содержащего возрастающую тенденцию.
Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер (регулярные колебания в теч-ие года), поскольку экономическая деятельность ряда отраслей зависит от времени года (например, цены на сельскохозяйственную продукцию в летний период выше, чем в зимний; уровень безработицы в курортных городах в зимний период выше по сравнению с летним). При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка, а также с фазой бизнес-цикла, в которой находится экономика страны. На рис. 6.1 б представлен гипотетический временной ряд, содержащий только сезонную компоненту.
Некоторые временные ряды не содержат тенденции и циклическую компоненту yt = f(ε), а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты. Пример ряда, содержащего только случайную компоненту, приведен на рис. 6.1 в.
М.б. ряды, в к-х отсутствует тенденция и периодические колебания. Такие ряды часто называют стационарными:
В эконометрике чаще встречаются ряды с тенденцией yt = f (T):
Очевидно, что реальные данные не соответствуют полностью ни одной из описанных выше моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты:
В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда:
yt = T + P + E
Модель, в которой врем. ряд представлен как произведение перечисл. компонент, назыв. мультиплика-тивной моделью врем. ряда. Выбор вида модели зависит от хар-ра период. колебаний:
если амплитуда сезонных колебаний одинакова, то можно рассматривать аддитивную модель, в к-рой значения сезонной (P) предполагаются постоянными для различных циклов.
если амплитуда сезонных колебаний резко меняется во времени, то строится мультипликативная модель, к-рая ставит уровни ряда в зависимость от значений сезонной компоненты.
В аддитивной модели компоненты ряда выражены в тех же ед-цах, что и изучаемый в динамике признак (y- тонн, тенд- тонн, колеб- тонн).
В мультипликативной модели периодические и случайные составляющие обычно выражены в относительных величинах (коэфф-т сезонности).
Основная задача эконометрического исследования отдельного временного ряда — выявление и придание количественного выражения каждой из перечисленных выше компонент, с тем чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

2. Аналитическое выравнивание временных рядов.

дной из задач исследования экономического временного ряда является выявление основной тенденции развития изучаемого процесса, т.е. выбор аналитической функции, которая описывает данных процесс или явление.

При выборе функции сначала определяют её вид. Наиболее часто используются функции следующих типов:

1) линейная y=b₀+b₁t

2) полиномиальная y=b₀+b₁t+b₂t²+...+b_ntⁿ

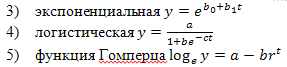При выборе соответствующей функции f(t) используют содержательный анализ, который может установить характер динамики изучаемого процесса.

При выборе функции f(t) используют графическое изображение временного ряда. После выбора типа функции определяются неизвестные параметры этой функции с помощью МНК (сумма квадратов отклонений в узловых точках стремится к min). Кроме того, при выборе аналитической функции следует ориентироваться на возможно более простой аналитический вид этой функции.

При использовании МНК значения временного ряда y_t рассматриваются как зависимые переменные, а время t – как факторная или объясняющая переменная.

Предположим, что динамика ряда описывается линейной функций y=b₀+b1t. Тогда согласно МНК для определения неизвестных параметров b₀ и b₁ используется система нормальных уравнений:

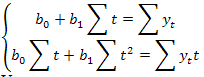
Учитывая, что значение переменной t образует натуральный ряд чисел от 1 до n, суммы t и t² можно вычислить по формулам:

Другим методом выравнивания временного ряда, является метод скользящих средних. Он основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. При этом сам выбранный интервал времени «скользит» вдоль ряда. Получаемый таким образом ряд скользящих средних ведет себя более гладко, чем исходный ряд, из-за усреднения отклонений рада.

Практическое занятие №8,9

Задание 1. Logit-модель была применена к выборке, в которой y =1, если количество занятых в фирме выросло (y =0 – в противном случае), х ₁ – доход фирмы, в млн. $; х ₂=1, если фирма относится к области высоких технологий (х ₂=0 – в противном случае). Получена следующая модель:

Требуется определить оценку вероятности роста занятости для фирмы высокотехнологичной фирмы А с доходом в 5 млн. $ и для фирмы Б, не относящейся к сфере высоких технологий и имеющей доход 7 млн. $.

Задание.2

Имеется выборка, состоящая из 528 наблюдений, в которой y =1, если заработная плата работника ниже 5$ в час (y =0 – в противном случае). Предполагается, что уровень заработной платы зависит от следующих факторов: х ₁ – образование, лет; х ₂ – пол (1–женский, 0 – мужской); х ₃ – опыт работы, лет. В табл. 10.1 приведены коэффициенты, полученные при оценке линейной регрессии y от х ₁, х ₂ и х ₃ с помощью МНК, и при оценке Logit-модели с помощью нелинейного МНК.

Таблица 10.1

	Коэффициенты
	линейной регрессии	Logit-модели	Выборочные средние
	0,94	5,87
х 1	–0,05	–0,56	13,09
х 2	0,15	1,26	0,46
х 3	–0,01	–0,06	17,66

Требуется:

1. Определить на основе Logit-модели, оценку вероятности для мужчины и для женщины, имеющих 12 лет образования и 15 лет опыта работы, оказаться низкооплачиваемыми работниками.

2. Определить на основе Logit-модели, изменение оценки вероятности быть низко оплачиваемым работником для мужчины с характеристиками из п. 1, если он проучится на один год больше.

3. Ответить на вопросы п. 1–2 с использованием линейной регрессионной модели.

Задание.3

Имеется выборка, состоящая из 528 наблюдений, в которой y =1, если работник состоит в профсоюзе (y =0 – в противном случае). Предполагается, что членство в профсоюзе зависит от следующих факторов: х ₁ – образование, лет; х ₂ – пол (1–женский, 0 – мужской); х ₃ – опыт работы, лет; х ₄ – опыт работы в квадрате. Выборочные средние равны

На основе выборочных данных была получена следующая Probit-модель:

Требуется определить, насколько снижается вероятность быть членом профсоюза в расчете на год дополнительного образования.

Задание.4

Имеется набор данных, состоящий из 6 наблюдений.

y
x	–1	–2

Требуется:

1. Оценить линейную модель вероятности с помощью МНК. Рассчитать R ².

2. Использовать оцененную модель для разделения индивидуумов на 2 группы. Рассчитать количество случаев правильного отнесения к соответствующей группе, применяя следующее правило классификации:

группа I (y =1), если

группа II (y =0), если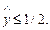

Сопоставьте долю правильного попадания и коэффициент детерминации.

Дата добавления: 2014-01-03