Обоснование алгоритма. Прежде всего, заметим, что реализация алгоритма состоит из конечного числа шагов

Прежде всего, заметим, что реализация алгоритма состоит из конечного числа шагов. В самом деле, п. 3° может применяться лишь конечное число раз, так как на каждом шаге величина потока увеличивается, по крайней мере, на единицу. Вместе с тем величина любого потока не может превзойти суммарной пропускной способности дуг, инцидентных выходу сети .

Процесс присвоения меток в силу того, что каждый раз получают метку еще неотмеченные вершины, конечен. И, наконец, в п. 5° поток 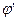обладает большей величиной, чем 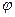. Это вытекает из того, что по определению вершины 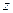и правил п. 4° б) дугам, входящим в 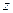, может быть присвоен только знак «+».

Получаемая по правилу 3° функция 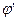— поток. Это непосредственно следует из того, что 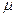— путь. В соответствии с правилом п. 5° строится также поток. Чтобы доказать это утверждение, рассмотрим три соседние вершины последовательности 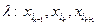. В силу правила 4° б) возможны только ситуации, представленные на рис. 10. Но в этих ситуациях 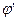— поток.

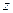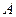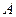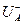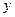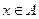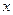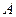Пусть процесс, описанный в п. 4° б), приводит к тому, что вершина не получает метки. Обозначим через множество непомеченных вершин. В силу того, что , множество определяет разрез сети. Каждая дуга соединяет помеченную вершину с непомеченной вершиной . Вершина может остаться непомеченной при условии, что . Аналогично, на каждой дуге (выходящей из ) выполняется равенство 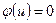, поэтому справедливы соотношения:

.

В силу леммы это означает, что поток 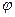обладает наибольшей величиной.

Рис. 10

Проведенное рассуждение совместно с леммой составляют доказательство следующей теоремы.

Дата добавления: 2014-01-03