Понятие общерекурсивной функции

Для каждой частично рекурсивной функции 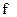существует механический процесс, посредством которого любое натуральное число 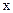перерабатывается в значение 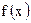функции 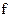. Этим процесс продолжается бесконечно, не давая окончательного результата, тогда и только тогда, когда значение функции 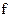в точке 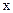не определено. Таким образом, всюду определенная частично рекурсивная функция - это функции, для вычисления значений которой существует алгоритм, обрывающейся через конечное число шагов для любого начального числа. Алгоритмы, которые перерабатывают в определенное число любое заданное число, играют особую роль в теории алгоритмов. Вместе с ними особое положение в теории рекурсивных функций занимают всюду определённые частично рекурсивные функции. Такие функции называются общерекурсивными.

Можно доказать, что многие известные арифметические функции являются примитивно рекурсивными. Среди них, например, неполное частное и остаток при делении натурального числа 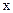на число 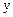. Примитивно рекурсивной является характеристическая функция множества всех простых чисел натурального ряда.

Одна из наиболее известных арифметических функций - функция 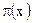- равная числу простых чисел, не превосходящих 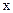. Эта функция примитивно рекурсивная.

Если значения примитивно рекурсивной, общерекурсивной или частично рекурсивной функции изменить лишь на конечном множестве точек, то новая функция будет снова примитивно рекурсивной, общерекурсивной или соответственно частично рекурсивной.

Примитивно рекурсивными будут следующие множества натуральных чисел:

1) любая конечная совокупность чисел;

2) множества чисел вида ;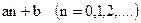

3) множества чисел вида 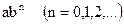и т.д.

Дата добавления: 2014-01-03