Машины Тьюринга

Важный и широкий класс алгоритмов был описан Тьюрингом и Постом в 1936 - 1937 г. Алгоритмы этого класса осуществляются особыми машинами, называемыми сейчас машинами Тьюринга-Поста или просто машинами Тьюринга.

Машины Тьюринга копируют работу человека, вычисляющего по заданной программе.

В 1936 г. Пост и Тьюринг одновременно и не зависимо друг от друга ввели в рассмотрение гипотетическую (не существующую) машину для определения алгоритма. Основная мысль их заключалась в том, что предписания всякого алгоритма может выполнить некоторая подходяще устроенная машина. Машины Поста и Тьюринга несущественно отличаются, но их возможности одинаковы и сегодня их называют машинами Тьюринга.

Машина Тьюринга состоит из следующих частей:

а) Конечная лента, разбитая на конечное число ячеек. В процессе работы машина к существующим ячейкам может пристраивать новые ячейки, так что ленту можно считать потенциально бесконечной в обе стороны.

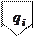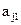
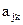
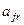
Каждая ячейка ленты может находиться в одном из конечного множества состояний. Эти состояния будем обозначать символами: 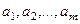. Множество этих символов называется внешним алфавитом машины, а сама лента часто называется внешней памятью машины. Клетки в фиксированном состоянии называются пустыми. В процессе работы машины ячейки ленты могут изменять свои состояния, но могут и не менять их. Все вновь пристраиваемые ячейки пристраиваются пустыми. Лента считается направленной и её ячейки просматриваются слева направо. Таким образом, если в какой-то момент времени лента имеет 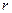ячеек, и внешний алфавит машины состоит из символов 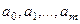, то состояние ленты полностью описывается словом 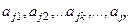, где 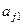- состояние первой ячейки (слева), 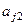- состояние второй ячейки и т.д.

б) Внутренняя память машины - это устройство, которое в каждый рассматриваемый момент находится в некотором состоянии. Число возможных состояний внутренней памяти конечно и для каждой машины фиксированное. Состояние внутренней памяти мы будем обозначать символами 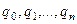, не входящими во внешний алфавит машины. Состояние внутренней памяти называют внутренними состояниями машины. Символы внутренней памяти называют внутренним алфавитом машины. Одно из внутренних состояний называется заключительным и в работе машины играет особую роль. Символ, обозначающий заключительное состояние машины будем обозначать: 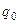и называть «стоп» - символом.

в) Управляющая головка. Это устройство, которое может, перемещаться вдоль ленты так, что в каждый рассматриваемый момент времени оно находится в определённой ячейке ленты. Иногда, наоборот считают управляющую головку неподвижной, а движущейся частью считают ленту. Тогда считают, что в управляющую головку вводится то одна, то другая ячейка ленты. Если какая-нибудь ячейка находится в управляющей головке, то говорят, что машина в данный момент обозревает эту ячейку.

г) Механическое устройство. Предполагается, что машина снабжена особым механизмом, который в зависимости от состояния воспринимаемой ячейки и состояния внутренней памяти может изменить состояние внутренней памяти и одновременно либо изменить состояние воспринимаемой ячейки, либо сдвинуть управляющую головку в соседнюю справа ячейку. Если управляющая головка находится в самой правой ячейке и по ходу работы машина должна сдвинуть управляющую головку в соседнюю справа отсутствующую ячейку, то предполагается, что, сдвигая головку, машина одновременно пристраивает недостающую ячейку в пустом состоянии. Аналогично работает машина и в случае, когда головка воспринимает самую левую ячейку и по ходу дела машине надо сдвинуть головку ещё левее.

Наконец, если в какой-то момент времени внутренняя память машины приходит в заключительное состояние 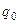, то дальнейших изменений в машине не происходит и машина называется остановившейся. Может случиться, что в машине не будет происходить никаких изменений и при каком-то другом внутреннем состоянии 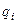. Однако в этом случае машина не считается остановившейся, считают, что в этом случае машина продолжает работать "вечно".

По определению, состоянием машины Тьюринга или её конфигурацией называется совокупность, образованная последовательностью 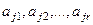состояний всех ячеек ленты, состоянием внутренней памяти 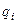и номером к воспринимаемой ячейки .

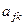Все эти данные можно записать одним словом 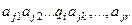, которое мы будем называть машинным словом, описывающим указанное состояние машины. Таким образом, каждое машинное слово содержит лишь одно вхождение символа 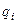из внутреннего состояния. Этот символ 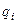может быть самым левым в машинном слове, но не может быть самым правым, т.к. справа от него должен помещаться символ состояния обозреваемой ячейки.

С помощью такого «виртуального» устройства можно решать различные алгоритмические задачи. Машина Тьюринга – это пример того, что даже очень сложные алгоритмы могут быть реализованы на очень простых устройствах.

Таким образом, машина Тьюринга - это множество, состоящее из пяти объектов (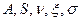), где конечное множество А – это входной и выходной алфавит, символы этого алфавита могут быть записаны в ячейках ленты; конечное множество S – это множество внутренних состояний машины; 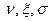- функции, определяемые следующим образом:

1) 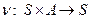- это функция перехода в следующее внутреннее состояние,

2) 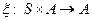- это функция выхода,

3) 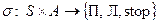- это функция, регулирующая движение ленты, или ее остановку.

Все эти функции зависят от того, в каком внутреннем состоянии в данный момент находится машина, и от считываемого с ленты символа.

Машина работает дискретно, по тактам.

Управляющая головка обозревает ячейку ленты, в которой записан символ 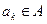. Находясь в состоянии 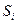, функция 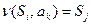переводит машину в новое внутреннее состояние 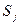; головка стирает символ 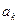, записанный в ячейке и записывает на ней новый символ, равный 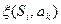, который может совпадать с прежним, и наконец, в зависимости от значения функции 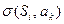(П, Л или останов.) головка сдвигается в соседнюю правую ячейку, если 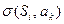= П, в соседнюю слева ячейку (если 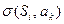=Л), или машина прекращает работу (если 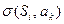= останов.)

Таким образом, программа работы машины состоит из тактов, каждый такт можно записать в виде:

,

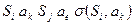где 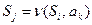, , 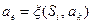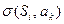=П, Л или останов.

Всякая программы работы машины – это конечная последовательность таких тактов.

На машинах Поста и на машинах Тьюринга оказалось возможным осуществить все алгоритмические процессы, которые когда-либо описывались математиками.

Список литературы.

1) Н. Я. Виленкин, Комбинаторика, «Наука», М., 1969.

2) М. Холл, Комбінаторика (пер. с англ.).

3) В. В. Белов, Е. М. Воробьев, В. Е. Шаталов, Теория графов, «Высшая школа», М., 1976.

4) О. Оре, Графы и их приложения, «Мир», 1965.

5) О. Оре, Теория графов (пер. с англ.), «Наука», 1968.

6) А. Гилл, Введение в теорию конечных автоматов, М., «Наука», 1966.

Учебное издание

курс лекций

по дискретной математике

2 семестр

(для студентов, специальности «Прикладная математика», «Компьютерные системы и сети»)

Составители:

Вячеслав Викторович БАРАБАШ

Елена Юрьевна ЧАЛАЯ

Авторский оригинал-макет

Издательство Восточноукраинского национального
университета имени Владимира Даля

Адрес издательства: 91034, г. Луганск, кв. Молодежный, 20а

Телефон: [phone], факс. [phone]

E-mail: [e-mail] http: www.snu.edu.ua

Дата добавления: 2014-01-03