Десятичный состав числа

а) состав однозначного числа, двузначного и любого другого;

5 10 12 3 136

/ \ / \ / \ / | \ / \

3 2 7 3 5 7 1 1 1 72 64

б) представление заданного числа в виде суммы разрядных слагаемых связано с выделением его десятичного состава:

12 106 136

/ \ / \ / | \

10 2 100 6 100 30 6

Моделируется с помощью карточек вида: [100], [30], [6].

9) Принцип поместного значения цифр - один и тот же знак (цифра) обозначает одно и то же количество единиц различных разрядов в зависимости от того, на каком месте (позиции) в записи числа стоит этот знак (цифра).

10) Класс - объединение трёх последовательных разрядов, начиная с разряда единиц.

11) Принцип ПОР - принцип поклассового объединения разрядов.

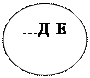Подпишите каждый из обозначенных на рисунке классов.

12) Сравнение чисел - установление отношений "равно",

"больше", "меньше".

Способы сравнения чисел:

- на основе сравнения множеств;

- по месту в N0: 3<4, a 4>3;

- по составу числа: 4>3, т.к. 4=3+1;

- по десятичному составу числа

37>32, 37>23, потому что…

- по количеству цифр

**<***, 7**<8**, потому что…

13) Свойства N0 - бесконечность, дискретность, упорядоченность.

Числовой луч, лента чисел, масштабная линейка - это модели множества целых неотрицательных чисел.

Число 10 в сотой степени - гугол (американский математик и педагог Кастнер) - граница исчисляемого мира, т.к. во всей Вселенной нет ничего больше, чем гугол.

Например, объём земного шара не превышает 10 в тридцатой степени миллиметров кубических.

Отношение размеров Вселенной и атомного ядра всего лишь примерно 10 в сороковой степени.

2. Цель и задачи изучения чисел

Цель - усвоение нумерационных понятий, способов чтения и записи чисел, т.е. овладевание языком математики.

Задачи: 1-13, а также:

- знакомство с источниками получения натуральных чисел, а значит с различными функциями натурального числа;

- формирование навыка счета по одному и разрядными единицами.

3. Особенности традиционной системы изучения чисел.

1. Понятие числа формируется на теоретико-множественной основе (Неявно: понятие "множество", "взаимно-однозначное отображение", "эквивалентность", "равномощность". Используется только на практическом уровне.)

2. Изучение чисел строится по принципу концентричности.

Какие концентры? Возможны ли другие? Почему концентры связаны именно с числом 10?

Это означает:

- перенос уже имеющихся знаний в новую, более широкую область чисел, а значит углубление и обобщение знаний;

- расширение имеющихся знаний (введение принципиально новых знаний).

Как это отражено в ОС №12 "Изучение нумерации"?

Почему одни лучи пронизывают все концентры, а другие нет?

- систематизация знаний.

Дата добавления: 2014-01-03