Способы нахождения табличных результатов

Проблема выбора пути

I путь в дореволюционной школе. Вспомните метод изучения чисел Грубе, «Арифметику» Магницкого.

II путь используется повсеместно уже многие десятилетия.

III путь практикуют некоторые учителя по мере овладения учащимися знаниями о способах составления таблиц.

Проблема последовательности изучения таблиц для каждого частного случая:

а+1 (2,…,9) – по постоянному второму слагаемому;

а·2 (3,…,9) или 2 (3,…,9)·а – по постоянному II или I множителю;

2, 3,…, 9 или 9,8,…, 2 или 9, 7, 2…? (традиционная, Пиядин, Давыдов, Истомина).

2. Анализ приёмов нахождения табличных результатов

1. Эмпирические (практические) – универсальные, но трудоёмкие.

Как именно находятся при этом результаты?

2. Логические:

а) для сложения и вычитания - прибавление и вычитание по частям,

б) для умножения - переход к сложению одинаковых слагаемых,

в) для деления - основанный на взаимосвязи деления с умножением.

Эти способы тоже универсальные, т.е. применимые к любой паре чисел, но для некоторых пар чисел рациональными являются другие ВП.

Например: 3+7, 3·7, 9-6.

Как вычислять легче?

Способы нахождения табличных произведений:

1) вычисление суммы одинаковых слагаемых;

2) используя предыдущий табличный результат;

3) группировка слагаемых – 2·7=2·5+2·2;

4) перестановка множителей – 2·7=7·2;

5) используя последующий результат – 2·4=2·5-2.

А для таблиц сложения? (2; 4; 5)

Каждый из названных способов нахождения табличных результатов имеет свое теоретическое обоснование, т.е. ответ на вопрос, почему так можно вычислять, даёт ответ математическая наука.

Приёмы сложения и вычитания по частям основаны на правилах:

а+(в+с)=(а+в)+с-ассоциативный закон сложения, и а-(в+с) =(а-в)-с ‑правило вычитания суммы из числа

Например: 9+4=10+3=13; 12-7=10-5=5

1 3 2 5

По действующей программе уровень овладения учащимися этими правилами – интуитивный, поэтому при составлении таблиц сложения и вычитания используются преимущественно эмпирические методы обучения.

Для вычитания как в пределах 10, так и в пределах 20 во многих случаях рациональным является прием, основанный на правиле нахождения неизвестного слагаемого

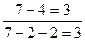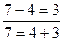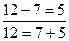Например: или ; или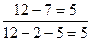

Это правило, переместительные законы сложения и умножения и др. теоретические основы названных ВП рассматриваются в НКМ явно (на экспериментальном или на логическом уровнях), а потому при введении таких ВП используются как эмпирические, так и логические – дедуктивные методы обучения.

Например: 2·5=10 5·2=10 и таблица начинается с 5·5

18=3·6 18:3=6 и 18:6=3

И на одном уроке можно составить сразу две таблицы деления.

3. Содержание подготовительной работы к составлению таблиц

Содержание подготовительной работы к составлению той или другой таблицы определяется исходя из анализа тех ВП, которые будут использоваться для нахождения табличных результатов.

Например: а) Сложение в пределах 10 (ОС № 13)

+1 - конкретный смысл сложения, принцип n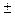1, последовательность чисел в N.

+2,3,4 - состав чисел I пятка, предшествующие таблицы.

+5,6,7,8 – переместительный закон сложения, оперативное правило, предшествующие таблицы.

б) Сложение с переходом через 10.

Состав чисел первого десятка, сложение в пределах 10, десятичный состав.

9+4=

1 3

в) Табличное деление.

Конкретный смысл деления, термины, взаимосвязь деления с умножением, правило нахождения неизвестного множителя.

Находит ли отражение содержание подготовительной работы в опорных схемах?

4. Особенности уроков по составлению таблиц

1.Учащиеся привлекаются к активному участию в составлении таблиц.

(Предметно-практическая деятельность. Всё, к чему готовы делают самостоятельно. Зона актуального развития.)

2. На уроке используются необходимые средства наглядности.

Например, для нахождения табличных произведений: числовые фигуры, записи на доске и в тетради, модель 1 дм² и прямого угла.

3. Применяют разные способы нахождения результатов.

4. Обосновывают, доказывают (практическим или логическим способами) правильность вычислений.

Например: 7-3=4, 24:4=6

Как доказать?

5. Таблица записывается на доске и в тетради.

6. Заучивание таблиц начинается на этом же уроке.

На одном и том же уроке можно составлять только одну таблицу (например: □+2 □ или 3·□) или связку таблиц (например, □+2 □ и □-2; 3·□ и □3, а также две таблицы деления).

5. Система работы по закреплению знания таблиц и формированию навыка воспроизведения по памяти табличных результатов

Какую бы методическую систему мы не избрали, работа с учащимися по заучиванию таблиц занимает исключительно важное место. Знание таблиц – это фундамент, база для овладения техникой быстрых и правильных устных и письменных вычислений. Именно этот факт является мотивом для заполнения таблиц.

Особенности сохранения и воспроизведения информации, хранящейся в памяти, зависят от того, как организовано запоминание.

И непроизвольное, и произвольное запоминание зависят от эмоционального отношения и интереса (удивление, восторг) к изучаемому материалу → создавать благоприятные условия.

Например, соревнование с калькулятором, со счетом на пальцах (римская школа).

Важным условием запоминания является включение в работу разных видов памяти: зрительной (физиологи утверждают, что зрительный анализатор в 800 раз мощнее слухового); слуховой, образной, словесно-логической (вербальный) → упражнения по таблицам должны быть разнообразны по видам деятельности учащихся: вслух, письменно, с объяснением, в игре и т.п.

В воспроизведении табличных результатов типичными являются ошибки памяти учащихся:

1) называют ответ соседнего в таблице примера: 6+4=9, 4·9=32, 32:4=7, 36:9 =5 (36:9=6);

2) смешивают примеры, результаты которых близки в натуральном ряду: 3·7=28, 69=56, 7·8=54.

Самые трудные для запоминания случаи умножения

7·8 6·9 8·8 7·9

Следовательно, их следует чаще включать в содержание обучения.

б) произведения с равными значениями:

18= □·□, 24=□·□, 12=□·□

3) смешивают правила оперирования с числами 0 и 1: 5·1=6, 5·0=5 и другие подобные случаи.

В работе над табличными случаями эффективны те же методические приемы, что и в работе над внетабличными, когда запомнить надо не результат, а способ вычислений, потому что речь идет об одном и том же познавательном процессе – запоминании.

Но есть и различия: специальное внимание уделяется отработке знания состава чисел из двух слагаемых; из двух множителей, т.к. это важный шаг к выполнению обратных действий и прочному запоминанию производных таблиц.

С этой целью полезно:

1) читать и запоминать табличные равенства слева направо и справа налево: 2·6=12 и 12=2·6; 3+4=7 и 7=3+4;

2) предлагать связки взаимообратных заданий (УДЕ):

3·8= □, 24=□·8, 3·□ =24

8·9=:8=9 9·8=:9=8

8·9=:8=9 9·8=:9=8

Другие специальные приемы в их логической последовательности законспектировать (ксерокопировать) в свою методическую копилку(см.: Медведская В.Н., Гудалина Т.И. Лабораторный практикум, с.94).

В Римской школе заучивались только таблицы умножения на числа 2, 3, 4,5. Все остальные произведения находили путем счета на пальцах.

Дано: a>5 и b>5.

Найти: а·в.

Дата добавления: 2014-01-03