Алгоритм проверки

1. Подставь найденное число в уравнение

2. Выполни действия над числами

3. Сравни значения левой и правой частей уравнения

4. Сделай вывод

Предупреждать формальный подход к проверке.

Обязательно ли проверять каждое уравнение?

Решение уравнений является мощным средством решения текстовых задач.

В начальном обучении осуществляется пропедевтическая работа в этом направлении:

― составление числовых выражений по текстам задач;

― разъяснение смысла каждого отдельного выражения, соответствующего условию конкретной задачи;

― составление выражений с переменной по тексту задачи

Женщин―а

Мужчин―?, на 20 больше? а+(а+20)

― составление уравнений по тексту задачи с отвлеченными числами: ”Я задумала число х∙4=36 умножила его на 4 получила 36. Какое число я задумала?”;

― составление уравнений по текстам сюжетных задач, сначала простых, затем― составных.

Как решать задачу алгебраическим способом

1. Восприятие и осмысление (как обычно, возможно, с использованием моделей разного вида).

2.-3. Поиск и составление плана решения. Решение уравнения.

- Установи, что известно и что неизвестно

- Обозначь одно из неизвестных чисел буквой (х)

- По условию задачи составь соответствующие выражения

- Найди условие, позволяющее составить равенство

- Составь уравнение

- Реши уравнение

- Дай ответ на вопрос задачи

Ответ на вопрос задачи ― это конкретизация полученного числа в соответствии с содержанием задачи.

4. Проверка задачи (а не уравнение)

Найденное значение переменной подставляется в условие задачи, а не в уравнение.

В обучении можно использовать принцип раздельного формирования умственных действий; то есть ставить на уроке операционные цели - учить:

― находить в тексте известные и неизвестные (явные и неявные);

― составить разные выражения, имеющие смысл для данной задачи;

―находить условия, позволяющие составить уравнение, то есть соединить знаком “=” математические выражения;

― составлять уравнения по тексту сюжетной задачи;

― составлять сюжетные задачи по уравнению;

― решать задачи алгебраическим способом.

При составлении уравнений нужно широко использовать иллюстрацию, чертежи, таблицы, схемы и другие модели, опираться на конкретные представления по содержанию задачи.

7. Методика работы над неравенствами с переменной

Неравенство с переменной — это предикат и потому самый элементарный способ их решения – способ подбора.

Поскольку работа с неравенствами в начальном курсе математики направлена в основном на формирование понятия “переменная”, способ подбора — основной способ их решения.

В ходе решения неравенств с переменной осуществляется закрепление и совершенствование ЗУНов по арифметике:

1) □ >5, х<20, 9<□<15, 348-a<348-216

Опора – числовая прямая.

2) 31-а>20, k∙7<40

а) Выбрать из заданного множества значений переменной.

б) Назвать несколько решений или все решения (на основе интуитивного знания об изменении результатов арифметических действий в зависимости от изменения одного из его компонентов).

3) 428>56∙x 852:y<284, то есть с многозначными числами сводится к решению уравнения.

Когда будет “ равно”? Как рассуждают учащиеся?

x=428:56 y=852:284

428 |56 852 | 283

392 |7 852 | 3

36 0

x=7 y=3

Ответ:7, 6, 5, …, 1 Ответ: 4, 5, …, 854

8. Функциональная пропедевтика в начальном обучение математике

Понятие функции, функциональной зависимости, соответствия является одним из важнейших в математике.

V x є Х 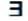! y є Y y є f(x)

В начальном курсе математики школьники встречаются с функциями, заданными разными способами:

— словесный (в текстовых задачах);

— табличный

а
а∙3

— аналитический, то есть формулой

“Найти значение выражения (а+6)∙а, если а=1, 2, 3”, где {1, 2, 3} – множество определения функции.

— графический, то есть указанием пар вида (х; y), где хєХ, a yєY или точек на координатной плоскости.

Найдите такие задания в школьных учебниках.

Программой предусмотрено ознакомление младших школьников с пропорциональной зависимостью (при решении текстовых задач):

Ст=ц∙к, S=a∙b, S=V∙t и др.

Наблюдаются некоторые свойства линейной, прямо и обратно пропорциональной функций, свойства возрастания и убывания.

Подчёркивать: изменение одной величины ведёт к изменению другой величины.

Дата добавления: 2014-01-03