Элементарные методы обработки расчетных данных

При изучении совокупности значений изучаемых величин, помимо средних, используют и другие характеристики. При анализе больших массивов данных обычно интересуются двумя аспектами:

1. величинами, которые характеризуют ряд значений как целого (средние величины, середина интервала, мода и медиана);

2. величинами, которые описывают различия между членами совокупности, т.е. характеристиками разброса (вариации) значений.

Середина интервала:

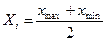
Мода – такое значение изучаемого признака, которое среди всех его значений встречается наиболее часто. Если все значения встречаются по одному разу или равное количество раз, такая совокупность является безмодальной.

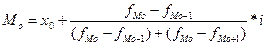
x₀ – нижняя граница модального интервала;

f_Mo – частота в модальном интервале;

f_Mo-1 – частота в предыдущем интервале;

f_Mo+1 – частота в следующем интервале за модальным;

i – величина интервала.

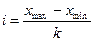
∆ расчета медианы по таблице

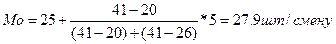
Медиана – такое значение изучаемой величины, которое делит изучаемую совокупность на две равные части, в которых количество членов со значениями меньше медианы равно количеству членов, которые больше медианы. Медиану можно найти только в совокупностях данных, содержащих нечетное количество значений.

В отличие от средней, медиана не зависит от крайних значений показателей. Например, если максимальное значение изучаемого показателя увеличится, то все средние возрастут вместе с ним. Медиана останется неизменной.

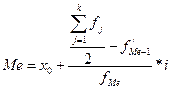
х₀ – нижняя граница интервала, в котором находится медиана;

f^`′_Me-1 – накопленная частота в интервале, предшествующем медианному;

f_Me – частота в медианном интервале.

Размах вариации:

R=Xmax-Xmin - характеризует разброс величины.

Var коэффициент вариации

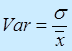Критическое значение 33%. Если Var >33 %, то совокупность нельзя назвать однородной.

Коэффициент асимметрии → 0, значит распределение величин симметрично:

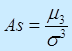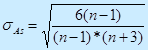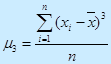Эксцесс:

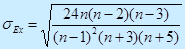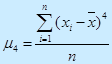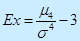Ex→0 означает нормальное распределение.

Большой положительный эксцесс означает, что в совокупности данных есть слабо варьирующее по данному признаку «ядро», окруженное редкими, сильно отстоящими от него значениями. Большое отрицательное значение показателя эксцесса говорит об отсутствии такого «ядра».

Среднее линейное отклонение (средний модуль отклонения):

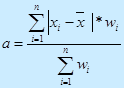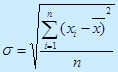Средневзвешенное среднее линейное отклонение:

Среднеквадратическое отклонение:

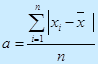
Дата добавления: 2014-01-03