Сущность и значение статистических моделейпроблема измерений в экономике

Статистика- быстроразвивающаяся отрасль науки, цель которой состоит в том, чтобы придать количественные меры эко­номическим отношениям.

В настоящее время эконометрика располагает огромным раз­нообразием типов моделей - от больших макроэкономических моделей, включающих несколько сот, а иногда и тысяч уравне­ний, до малых коинтеграционных моделей, предназначенных для решения специфических проблем.

Методы измерения развивались на протяжении всей истории человеческой цивилизации вместе с развитием математики и естественных наук. В прошлом веке математизация социальных и экономических наук дала новый импульс этим процессам. Проводилось серьезное переосмысление феномена измерений, осуществлялись продуктивные попытки разработать общие теории измерения.

Множества чисел, в которых проводится измерение, образуют измерительные шкалы. В концептуальном отношении Стивенсом выделено 4 основных типа шкал.

1) Номинальная шкала, шкала наименований, шкала классификаций. Объектам приписываются любые числа, которые играют роль простых имен и используются с целью различения объектов и их классов. Примеры: номера футболистов, числовые коды различных классификаторов. Основное правило такого измерения: не приписывать одно число объектам разных классов и разные числа объектам одного класса. В этой шкале вводится только два отношения: «равно» и «не равно». В ней измеряются объекты, которые пока научились или которые достаточно только различать.

2) Ординальная или порядковая, ранговая шкала. В этой шкале измеряются объекты, которые одинаковы или предпочтительнее друг друга в каком-то смысле. Принимаются во внимание только 3 отношения, в которых могут находиться числа этой шкалы: «равно», «больше», «меньше». Математическая структура шкалы определяется монотонновозрастающим преобразованием

3) Интервальная шкала. Шкала используется для измерения объектов, относительно которых можно говорить не только больше или меньше, но и на сколько больше или меньше. Т.е. в ней введено расстояние между объектами и, соответственно, определены единицы измерения, но нет пока нуля, и бессмысленнен вопрос о том, во сколько раз больше или меньше. Математическая структура шкалы:

f = aX + b,

где a > 0 (a — коэффициент изменения единицы измерения, b — «сдвиг» нуля). В этой шкале измеряются некоторые физические величины, например, температура. Если ночью по Цельсию было 5 градусов тепла, а днем — 10, то можно сказать, что днем теплее на 5 градусов, но утверждение, что днем в 2 раза теплее, чем ночью, бессмысленно.

В шкале Фаренгейта или Кельвина данное отношение совсем другое.

4) Шкала отношений. В ней по сравнению с предыдущей шкалой введен ноль (естественное начало шкалы) и определено отношение «во сколько раз больше или меньше». Математическая структура шкалы:

f = aX

(a — коэффициент изменения единицы измерения), a > 0.

Это обычная шкала, в которой проводится большинство метрических измерений. Первые два типа шкал неметрические, они используются в нефизическом измерении (в социологии, психологии, иногда в экономике), которое в этом случае называется обычно шкалированием. Метрическими являются шкалы двух последних типов. Экономические величины измерены, как правило, в шкале отношений.

Существуют различные виды измерений. С точки зрения дальнейшего изложения важно выделить два вида: прямые, или первичные, которые в физических измерениях иногда называют фундаментальными, и косвенные или производные.

Измерения 1-го вида сводятся к проведению эмпирических операций в непосредственном контакте с измеряемым объектом. Это — опрос, анкетирование, наблюдение, счет, считывание чисел со шкал измерительных приборов.

Измерения 2-го вида связаны с проведением вычислительных операций над первично измеренными величинами. Таким образом, в измерении используются и эмпирические, и вычислительные операции. Некоторые теоретики измерения склонны минимизировать роль вычисления и отделить собственно измерение, как преимущественно эмпирическую операцию, от вычислений. Однако грань между этими двумя понятиями достаточно расплывчата. Особенно — при экономических измерениях.

Специфические особенности экономических измерений можно свести в 5 групп.

1) Измеряться могут только операционально определенные величины. В экономике разработка операциональных определений величин — это сложный и неоднозначный исследовательский процесс теоретического характера. Теоретики постоянно дискутируют на темы измерения общих итогов экономического развития, экономической эффективности, производительности общественного труда, экономической динамики, инфляционных процессов, структурных сдвигов и т.д. Не выработано строгой и единой системы операциональных величин, однозначно представляющих эмпирическую экономическую систему. Одно из следствий такого положения, как уже говорилось, заключается в том, что каждому теоретическому понятию, как правило, соответствует несколько операциональных величин, отражающих различные точки зрения и используемых с разными целями.

Очень сильно различались системы статистического учета, сложившиеся в СССР и в мировой практике. В Казахстане к концу прошлого столетия, в целом, завершен переход на западные стандарты, но нельзя не видеть положительных моментов, имевшихся и в отечественной системе статистики. В мировой практике статистики к настоящему времени сложилась более или менее устойчивая, хотя и имеющая национальные особенности, система статистического отображения экономической действительности: Национальные Счета на макроуровне, Бухгалтерский учет в фирмах. И эти вопросы активно не дискутируются теоретиками. Но нет сомнений, что под воздействием накапливаемых изменений в общественной жизни «взрывы» таких дискуссий ждут впереди. Таким образом, экономические измерения, в отличие от многих физических, в очень сильной степени обусловлены теоретическими моментами.

2) Специфику экономическим измерениям создают и те особенности экономики, которые обсуждались выше в связи с пониманием особенностей статистики как науки и вероятностной природой экономических явлений. Короткие ряды наблюдений и неэкспериментальный характер данных очень затрудняют процесс измерения и нередко ставят под сомнение научную значимость его результатов. В процессе управляемого эксперимента можно изменить значение некоторой величины и определить, на что и каким образом она влияет, т.к. остальные величины-факторы остаются неизменными. Неэкспериментальные данные исключают возможность анализа «при прочих равных». В потоке наблюдений за «всеми сразу» величинами, как уже отмечалось, трудно уловить структуру взаимосвязей и измерить их интенсивность. Чисто эмпирически это, пожалуй, невозможно сделать. Это обстоятельство еще в большой степени увеличивает нагрузку на теорию, «силу абстракции» исследователя. И не добавляет надежности результатам измерения.

3) В экономике не существует таких объектов и не изобретено таких «линеек», совмещение которых позволило бы путем считывания чисел со шкалы определить объем валового внутреннего продукта или темп инфляции. Экономические измерения почти всегда косвенные, производные. Экономические величины определяются путем расчета, исчисления, формула которого задается операциональным определением величины. Более того, первичные измерения, имеющие в физике фундаментальное значение, в экономике, как правило, экономического характера не имеют. Это — счет, физические измерения веса, объема, длины, первичная регистрация цен, тарифов и т.д. Экономический характер они приобретают лишь после своей сверткив экономические величины.

4) В естественных науках единицы измерения: килограмм, метр, джоуль, ватт и т.д. — четко и однозначно определены. Специфические единицы экономических измерений: цены, тарифы, ставки, единицы полезности — постоянно меняются. Важно даже не то, что они меняются во времени, а то, что их изменения зависят от объема и пропорций тех величин, которые они призваны измерять. Если в структуре производства или в потребительском наборе доля какого-то продукта уменьшается, то его цена или полезность, как правило, растет. И наоборот. Учет такого рода зависимостей и изменчивости единиц измерения — очень сложная проблема, совершенно неизвестная в физических измерениях.

5) В процессе измерения инструмент взаимодействует определенным образом с объектом измерения, вследствие чего положение этого объекта может измениться, и результатом измерения окажется не та величина, которая имела место до самого акта измерения. Пример: если попытаться в темной комнате на ощупь определить положение бильярдного шара на столе, тот обязательно сдвинется с места. Эта проблема, так или иначе, возникает в любых измерениях, но только в экономических и, вообще, социальных измерениях она принимает угрожающие масштабы. Экономические величины складываются под воздействием определенной деятельности человека и характеризуют каким-то образом эту деятельность. Поэтому люди, как те, кто измеряет, так и те, чья деятельность измеряется, обязательно заинтересованы в результатах измерения. Взаимодействия в процессе измерения, возникающие по этим причинам, могут приводить к огромным отличиям получаемых значений измеряемых величин от их действительных значений. В физических измерениях влияние этого субъективного фактора практически отсутствует.

Под адекватностью измерений обычно понимают степень соответствия измеренных значений действительным или истинным. Разность этих значений образует ошибку измерения. Теория ошибок, основанная на теории вероятности и математической статистике, изучается в следующей части книги. Здесь рассматривается значение учета ошибок экономических измерений, причины этих ошибок, и приводятся некоторые примеры.

Любые измерения, а экономические в особенности, содержат ошибку. Точные величины суть не более, чем теоретические абстракции. Это происходит хотя бы в силу случайного характера величин. Исследователи располагают выборочными значениями величин и могут лишь приблизительно судить об их истинных значениях в генеральной совокупности. Измерения без указания ошибки достаточно бессмысленны. Фразу «Национальный доход равен 10 600 млрд. руб.» — если она не содержит сведений о точности или не подразумевает таких знаний у читателя (например, судя по количеству приведенных значащих цифр, ошибка составляет ± 50 млрд.руб.) — всегда можно продолжить: «или любой другой величине.

Ошибки обычно подразделяют на случайные и систематические. Для экономики можно ввести еще один класс ошибок: тенденциозные. Случайные ошибки — предмет строгой теории, здесь внимание сосредоточено на систематических и тенденциозных ошибках. В чем причины этих ошибок экономических измерений?

Каждая из 5 особенностей экономических измерений вносит в ошибку свою лепту, и немалую, сверх «обычной» ошибки физических измерений.

1) Ошибки теории. Операциональные определения экономических величин — продукт теории. И если теория неверна, то, как бы точно в физическом смысле не проводились измерения исходных ингредиентов, какими бы совершенными вычислительными инструментами не пользовались, ошибка —возможно очень большая — обязательно будет присутствовать в результатах измерения.

2) Ошибки инструмента, в данном случае — принятых статистических процедур расчета. Наибольшим дефектом в советской статистике страдали процедуры оценки динамики цен. Они скрывали реальные темпы инфляции.

Пример. На практике применяется два метода расчета национального дохода или валового внутреннего продукта (ВВП): потребительский — для определения использованного национального дохода, как суммы фактических объемов накопления и непроизводственного потребления, и производственный — для расчета произведенного национального дохода, как суммы чистой продукции (добавленной стоимости) по отраслям производства. Эти показатели жестко связаны между собой: их разница равна величине потерь и сальдо экспорта-импорта. Такая зависимость выдерживалась в государственной статистике только в текущих ценах. В сопоставимых ценах произведенный национальный доход устойчиво обгонял использованный — ежегодно на несколько миллиардов рублей. Если начать отсчет с начала 70-х годов, то к концу 80-х разрыв между произведенным и используемым национальным доходом достигал 1/5 последнего. Эти 100–150 млрд. руб. разрыва — одна из оценок ошибки расчета национального дохода в сопоставимых ценах.

В настоящее время в государственной статистике возникла в некотором смысле обратная проблема. ВВП, рассчитанный по производству, оказывается заметно меньшей величиной, чем рассчитанный по использованию. Причем разрыв также достигал в отдельных случаях 1/5 ВВП. Это происходит потому, что часть продукции производится в так называемой «теневой» экономике и не находит отражения в официальной статистике. Использование же продукции учитывается в более полных объемах.

3) Тенденциозные ошибки. Являются следствием субъективного фактора в процессе измерения. Искажение и сокрытие информации — элемент рациональной стратегии экономического поведения. Это общепризнанный факт, но в СССР, в силу значительной идеологической нагрузки на статистику, искажение информации, особенно итоговой, достигало удручающе больших размеров. По оценкам Г.И. Ханина реальный рост национального дохода за период с начала 1-й пятилетки (конца 20-х годов прошлого столетия) до начала 80-х годов прошлого века составлял не 90 раз, как по официальной статистике, а всего 7–8 (что тоже, кстати, очень неплохо). В современной официальной статистике такие ошибки также имеют место. Но, если во времена СССР совокупные объемы производства преувеличивались, то теперь они занижаются. Это — результат «бартеризации» экономики, выведения хозяйственной деятельности из-под налогообложения. Косвенным подтверждением этих фактов является то, что при резком сокращении общих (официальных) объемов производства в последнем десятилетии прошлого века объемы потребления электроэнергии, топлива, тепла, объемы грузоперевозок уменьшились гораздо в меньшей степени.

4) Ошибки единиц измерения. Имеется серьезное отличие понимания точности в физическом и экономическом измерении. Даже, если измерения точны в физическом смысле, т.е. правильно взвешены и измерены первичные величины, использована бездефектная теория для свертки этих величин, ошибки в экономическом смысле могут присутствовать и, как правило, присутствуют.

Дело в том, что практически всегда искажены по сравнению со своими истинными значениями наблюдаемые экономические единицы измерения: цены, тарифы и т.д. Особенно велик масштаб этих деформаций был в централизованной экономике. Влияние их на результаты измерения и, далее, на процессы принятия решений в СССР было огромно. Это стало особенно очевидным в конце горбачевской «перестройки», когда разные республики и территории бывшего СССР начали выдвигать взаимные претензии, рассуждая на тему о том, кому, кто и сколько должен. Если взять Западную Сибирь, то по официальным данным на конец 80-х годов XX века ее сальдо вывоза-ввоза было хоть и положительно, но очень невелико. Расчеты же в равновесных ценах давали цифру плюс 15–20 млрд. руб., а в ценах мирового рынка — плюс 25–30. Сложной и однозначно не решаемой оказывается проблема «очистки» итоговых за год показателей от факторов инфляции.

2 ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ И СВОЙСТВА, ВЫТЕКАЮЩИЕ ИЗ ЕЕ ОПРЕДЕЛЕНИЯ, КЛАССИФИКАЦИЯ СОБЫТИЙ

Под вероятностью в широком смысле понимают количественную меру неопределенности или число, которое выражает степень уверенности в наступле­нии того или иного случайного события.

Напри­мер, нас может интересовать вероятность того, что объем продаж некоторого продукта не упадет, если цены вырастут, или вероятность того, что строи­тельство нового дома завершится в срок.

Случайным называется событие, которое может произойти или не произойти в результате некото­рого испытания. В дальнейшем для простоты мы будем опускать термин «случайный».

Испытание (опыт, эксперимент) — это процесс, включающий определенные условия и приводящий к одному из нескольких возможных исходов. Исхо­дом опыта может быть результат наблюдения или измерения.

Единичный, отдельный исход испытания назы­вается элементарным событием.

Случайное событие может состоять из несколь­ких элементарных событий, подразделяющихся на достоверные, невозможные, совместные, несовместные, единственно возможные, равновозможные, противоположные.

Событие, которое обязательно произойдет в ре­зультате испытания, называется достоверным.

Например, если в урне содержатся только белые шары, то извлечение из нее белого шара есть событие дос­товерное; другой пример, если мы подбросим вверх камень, то он обязательно упадет на землю в силу действия закона притяжения, т. е. результат этого опыта заведомо известен. Достоверные события ус­ловимся обозначать символом W

Событие, которое не может произойти в резуль­тате данного опыта (испытания), называется не­возможным.

Извлечение черного шара из урны с белыми шарами есть событие невозможное; выпадение выигрыша на все номера облигаций в каком-либо тираже выигрышного займа также невозмож­ное событие. Невозможное событие обозначим Æ.

Достоверные и невозможные события, вообще го­воря, не являются случайными.

Несколько событий называются совместными, если в результате эксперимента наступление одного из них не исключает появления других. Например, при бросании 3 монет выпадение цифры на одной не исключает появления цифр на других монетах.

В магазин вошел покупатель. События «В мага­зин вошел покупатель старше 60 лет» и «В магазин вошла женщина» — совместные, так как в магазин может войти женщина старше 60 лет.

Несколько событий называются несовместными в данном опыте, если появление одного из них исключает появление других. Например, выигрыш, ничейный исход и проигрыш при игре в шахматы (одной партии) — 3 несовместных события.

События называются единственно возможными, если в результате испытания хотя бы одно из них обязательно произойдет (или 1, или 2, или... или все события из рассматриваемой совокупности событий произойдут; одно точно произойдет), Например, некая фирма рекламирует свой товар по радио и в газете. Обязательно произойдет одно и только одно из следующих событий: «Потребитель услышал о товаре по радио», «Потребитель прочитал о товаре в газете», «Потребитель получил информа­цию о товаре по радио и из газеты», «Потребитель не слышал о товаре по радио и не читал газеты». Эти 4 события единственно возможные.

Несколько событий называются равновозможными, если в результате испытания ни одно из них не имеет объективно большую возможность появления, чем другие. При бросании игральной кости появление каждой из ее граней — события равновозможные.

Два единственно возможных и несовместных события называются противоположными. Купля и продажа определенного вида товара есть события противоположные.

Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элементарных исходов.

Обозначим число благоприятствующих событию А исходов через М, а число всех исходов — N

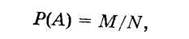(2.1)

где М — целое неотрицательное число, 0 < М < N.

Какой бы вид вероятности ни был выбран, для их вычисления и анализа используется один и тот же набор математических правил.

Свойства вероятности, вытекающие из классического определения:

1. Вероятность достоверного события равна 1, то есть Р(Ω) = 1.

2. Вероятность невозможного события равна 0, то есть Р(Ø) = 0.

3. Вероятность случайного события есть положительное число, заключенное между 0 и 1: 0 ≤ Р(А) ≤ 1.

4. Сумма вероятностей противоположных событий равна 1.

3 ФОРМУЛЫ ПОЛНОЙ ВЕРОЯТНОСТИ И БАЙЕСА. АПРИОРНЫЕ И АПОСТЕРИОРНЫЕ ВЕРОЯТНОСТИ

Часто мы начинаем анализ вероятностей, имея предварительные, априорные значения вероятностей интересующих нас событий. Затем из источников информации, таких как выборка, отчет, опыт и т. д., мы получаем дополнительную информацию об интересующем нас событии. Имея эту новую информацию, мы можем уточнить, пересчитать значения априорных вероятностей. Новые значения вероятностей для тех же интересующих нас событий будут уже апостериорными (послеопытными) вероятностями. Теорема Байеса дает нам правило для вычисления таких вероятностей.

Последовательность процесса переоценки вероятностей можно схематично изобразить так как на рисунке 3.1.

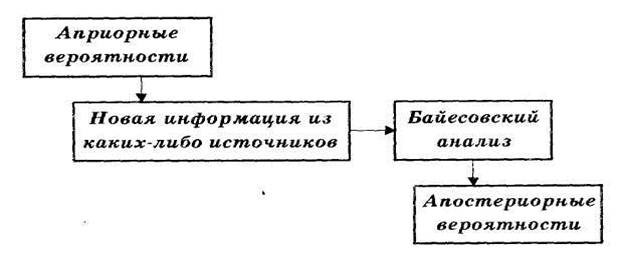
Рисунок 3.1 – Переоценка вероятностей

Пусть событие А может осуществиться лишь вместе с одним из событий Н₁, Н₂, Н₃,..., Н_n, образующих полную группу. Пусть известны вероятности Р(Н₁), Р(Н₂), Р(Н₃),..., Р(Н_i),..., Р(Н_п). Так как события H_i, образуют полную группу, то

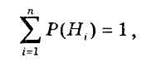(3.1)

а также известны и условные вероятности события А:

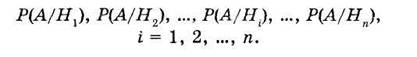
Так как заранее неизвестно, с каким из событий H_i произойдет событие А, то события H_i называют ги­потезами.

Необходимо определить вероятность события А и переоценить вероятности событий H_i сучетом полной информации о событии А.

Вероятность события А определяется как

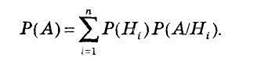(3.2)

Эта вероятность называется полной вероятностью.

Если событие А может наступить только вместе с одним из событий Н₁, Н₂, Н₃,..., Н_n, образую­щих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме произведений вероятностей каждого из событий Н₁, Н₂, Н₃,..., Н_n, на соответствующую ус­ловную вероятность события А.

Апостериорные вероятности гипотез вычисляются по формуле

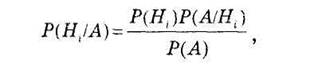(3.3)

Это — формулы Байеса (по имени английского математика Т.Байеса, опубликовавшего их в 1764 г.), выражение в знаменателе — формула полной вероятности.

4 ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЗАКОН РАСПРЕДЕЛЕНИЯ, ЕГО ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ. РАСЧЕТ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ СЛУЧАЙНОЙ ДИСКРЕТНОЙ ВЕЛИЧИНЫ

Величина, которая в результате испытания может принять то или иное значение, заранее неизвестно, какое именно, считается случайной.

Дискретной случайной величиной называется такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значе­ний есть случайное событие с определенной вероятностью.

Соотношение, устанавливающее связь между отдельными возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения дискретной случайной величины. Если обозначить возмож­ные числовые значения случайной величины X через х₁, х₂,..., х_п а через р_i = Р(Х = х_i) вероятность появления значения х_i, то закон распределения дискретной случайной величины Х выглядит следующим образом (таблица 3.1).

Здесь значения х₁, х₂,..., х_п записываются, как правило, в порядке возрастания. Таблица называется законом (рядом) распределен ия дискретной случайной величины X. Поскольку в его верхней строчке записаны все значения случайной величины X, то нижняя обладает следующим свойством:

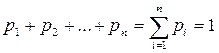(4.1)

Таблица 4.1 - Закон распределения дискретной случайной величины Х

хi	х1	х2	…	хn
рi	р1	р2	…	рn

Ряд распределения можно изобразить графически (рисунок. 4.1).

Если на рисунке 4.1 по оси абсцисс отложить значения случайной величины, по оси ординат — вероятности значений, полученные точки соединить отрезками прямой, то получим многоугольник распределения вероятностей (полигон распределения). Дискретная случайная величина может быть задана функцией распределения.

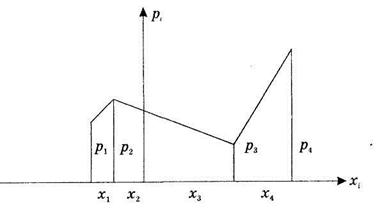
Рисунок 4.1 – Ряд распределения

Функцией распределения случайной величины X называется функция F(х), выражающая вероятность того, что X примет значение, меньшее чем х:

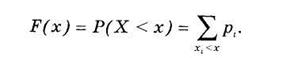(4.2)

Здесь для каждого значения х суммируются вероятности тех значений х_i, которые лежат левее точки х.

Функция F(х) есть неубывающая функция.

Для дискретных случайных величин функция распределения F(х) есть разрывная ступенчатая функция, непрерывная слева (рисунок 4.2):

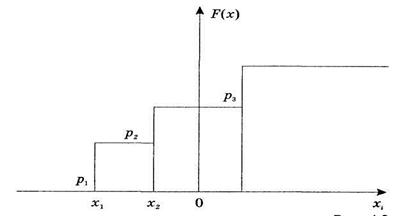
Рисунок 4.2 - Функция распределения F(х)

Вероятность попадания случайной величины X в промежуток от a до b (включая a) выражается формулой

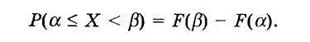(4.3)

Одной из важных числовых характеристик случайной величины X является математическое ожидание

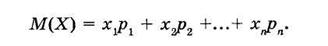(4.4)

М(Х) представляет собой среднее ожидаемое зна­чение случайной величины. Оно обладает следую­щими свойствами:

1) М(С) = С, где С – const;

2) М(СХ) = СМ(Х);

3) М(Х+У) = М(Х) + М(У), для любых Х и У;

4) М(ХУ) = М(Х) М(У), если Х и У независимы

Для оценки степени рассеяния значений случайной величины около ее среднего значения М(Х) = а вводятся понятия дисперсии D(Х) и среднего квадратического (стандартного) отклонения s (х). Дис­персией называется математическое ожидание квадрата разности (X — а),

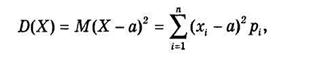(4.5)

где а = М(Х); s(х) определяется как квадратный корень из дисперсии:

s (х) =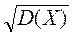. (4.6)

Для вычисления дисперсии можно также пользоваться форму­лой:

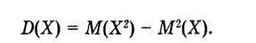(4.7)

Свойства дисперсии и среднего квадратического отклонения:

1) D(C) = 0, C = const

2) D(CX) = C²D(X), s(CX) = ê C ÷s (X);

3) D(X+Y) = D(X) + D(Y), s(X+Y) =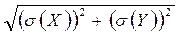

если X и У независимы.

Размерность величин М(Х) и s(Х) совпадает с размерностью самой случайной величины X, а размерность D(Х) равна квадрату размерности случайной величины X.

5 ВЫБОРОЧНЫЙ МЕТОД И СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЛЬНОЙ И ВЫБОРОЧНОЙ СОВОКУПНОСТЕЙ. ОПРЕДЕЛЕНИЕ И СВОЙСТВА ОЦЕНКИ

При проведении научных экспериментов невозможно проводить исследования по всей совокупности значений (генеральной совокупности), применение выборочных данных дает возможность экономии средств и затрат труда на получение и обработку информации. Объективную гарантию репрезентативности (представительности) полученной выборочной совокупности дает применение соответствующих научно обоснованных способов отбора подлежащих обследованию единиц.

Система правил отбора единиц и способов характеристики изучаемой совокупности исследуемых единиц составляет содержание выборочного метода.

Все единицы совокупности, обладающие интересующими исследователя признаками, составляют генеральную совокупность.

Часть совокупности, случайным образом отобранная из генеральной совокупности, - выборочная совокупность – выборка.

Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности – n.

Выборку называют репрезентативной (представительной), если она достаточно полно представляет изучаемые признаки и параметры генеральной совокупности. Для репрезентативности выборки важно обеспечить случайность отбора, с тем, чтобы все объекты генеральной совокупности имели равные вероятности попасть в выборку. Для обеспечения репрезентативности выборки применяют следующие способы отбора: простой отбор (последовательно отбирается первый, случайно попавшийся объект), типический отбор (объекты отбираются пропорционально представительству различных типов объектов в генеральной совокупности), случайный отбор – например, с помощью таблицы случайных чисел и т.п.

В эконометрике всегда известна только выборка из некоторого количества наблюдений случайной величины и по данным выборки можно рассчитать только выборочные, а не теоретические характеристики этой случайной величины

Проблема использования данных выборки для определения харак­теристик распределения может рассматриваться под разными углами зрения. Один из подходов называется оцениванием.

Пусть из генеральной совокупности извлекается выборка объемом п, причем значение признака х₁ наблю­дается т₁ раз, х₂ т₂ раз,..., х_к наблюдается т_к раз, Мы можем сопоставить каждому значению х_i относительную частоту т_i/п.

Статистическим распределением выборки называется перечень возможных значений признака х_i и соответствующих ему частот или относитель­ных частот (частостей) m_i (w_i).

Числовые характеристики генеральной совокупости, как правило, неизвестные (средняя, дисперсия и др.), называются параметрами генеральной совокупности (обозначают, например, 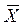или 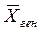, σ² _ген). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначается р.

По данным выборки рассчитывают числовые характеристики, которые называют статистиками (обозначают 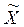, или 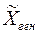, S², выборочная доля обозначается w). Статистики, получаемые по различным выборкам, как правило, отличаются друг от друга. Поэтому статистика, полученная из выборки, является только оценкой неизвестного параметра генеральной совокупности. Оценка параметра — определенная числовая характеристика, полученная из выборки. Когда оценка определяется одним числом, ее называют точечной оценкой.

В качестве точечных оценок параметров генераль­ной совокупности используются соответствующие выборочные характеристики. Теоретическое обосно­вание возможности использования этих выборочных оценок для суждений о характеристиках и свойствах генеральной совокупности дают закон больших чи­сел и центральная предельная теорема Ляпунова.

До сих пор мы предполагали, что имеется точная информация о рассматриваемой случайной переменной, в частности — об ее распределении вероятностей (в случае дискретной переменной) или о функции плотности распределения (в случае непрерывной переменной). С помощью этой информации можно рассчитать теоретическое математическое ожидание, дисперсию и любые другие характеристики, в которых мы можем быть заинтересованы.

Однако на практике, за исключением искусственно простых случайных величин (таких, как число выпавших очков при бросании игральной кости), мы не знаем точного вероятностного распределения или плотности распределения вероятностей. Это означает, что неизвестны также и теоретическое математическое ожидание, и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других теоретических характеристик генеральной совокупности.

Процедура оценивания всегда одинакова. Берется выборка из п наблюдений, и с помощью подходящей формулы рассчитывается оценка нужной характеристики. Нужно следить за терминами, делая важное различие между способом или формулой оценивания и рассчитанным по ней для данной выборки числом, являющимся значением оценки.

Оценка, способ оценивания (estimator) - общее правило, формула для получения приближенного численного значения какого-либо параметра по данным выборки, а значение оценки (estimation) - число, полученное в результате применения оценки к конкретной выборке; является случайной величиной, значение которой зависит от выборки.

Поскольку оценки являются случайными переменными, их значения
лишь по случайному совпадению могут в точности равняться характеристикам генеральной совокупности. Обычно будет присутствовать определенная ошибка, которая может быть большой или малой, положительной или отрицательной, в зависимости от чисто случайных составляющих величин х в выборке.

Хотя это и неизбежно, на интуитивном уровне желательно, тем не менее, чтобы оценка в среднем за достаточно длительный период была аккуратной. Выражаясь формально, мы хотели бы, чтобы математическое ожидание оценки равнялось бы соответствующей характеристике генеральной совокупности. Если это так, то оценка называется несмещенной. Если это не так, то оценка называется смещенной.

Смещение - разность между математическим ожиданием оценки и истинным начением оцениваемого параметра, а несмещенная оценка- оценка, имеющая нулевое смещение.

Несмещенность — желательное свойство оценок, но это не единственное такое свойство. Еще одна важная их сторона — это надежность. Конечно, немаловажно, чтобы оценка была точной в среднем за длительный период. Мы хотели бы, чтобы наша оценка с максимально возможной вероятностью давала бы близкое значение к теоретической характеристике, что означает желание получить функцию плотности вероятности, как можно более "сжатую" вокруг истинного значения. Один из способов выразить это требование — сказать, что мы хотели бы получить сколь возможно малую дисперсию.

Предположим, что мы имеем две оценки теоретического среднего, рассчитанные на основе одной и той же информации, что обе они являются несмещенными и что их функции плотности вероятности показаны на рисунке 5. Поскольку функция плотности вероятности для оценки В более "сжата", чем для оценки А, с ее помощью мы скорее получим более точное значение. Формально говоря, эта оценка более эффективна.

Эффективная оценка - несмещенная оценка, имеющая наименьшую дисперсию среди всех несмещенных оценок.

Важно заметить, что мы использовали здесь слово «скорее». Даже хотя оценка В более эффективна, это не означает, что она всегда дает более точное значение. При определенном стечении обстоятельств значение оценки А может быть ближе к истине. Однако вероятность того, что оценка окажется более точной, чем В, составляет менее 50%.

Мы уже выяснили, что для оценки желательна несмещенность и наименьшая возможная дисперсия. Эти критерии совершенно различ­ны, и иногда они могут противоречить друг другу.

Может случиться так, что имеются две оценки теоретической характеристики, одна из которых является несмещенной (А на рисунке 4.2), другая же смещена, но имеет меньшую дисперсию (В).

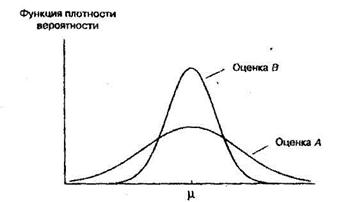
Рисунок 5.1 – Эффективные и неэффективные оценки

Оценка А хороша своей несмещенностью, но преимуществом оценки В является то, что ее значения практически всегда близки к истинному значению. Какую из них вы бы выбрали?

Данный выбор зависит от обстоятельств. Если возможные ошибки вас не очень тревожат при условии, что за длительный период они "погасят" друг друга, то, по-видимому, вы выберете А. С другой стороны, если для вас приемлемы малые ошибки, но неприемлемы большие, то вам следует выбрать В.

Формально говоря, выбор определяется функцией потерь, стоимостью сделанной ошибки как функцией ее размера. Обычно выбирают оценку, дающую наименьшее ожидание потерь, и делается это путем взвешивания функции потерь по функции плотности вероятности. (Если вы не любите риск, то можете также пожелать учесть дисперсию потерь).

Оценка А не имеет составляющей смещения, но имеет гораздо большую составляющую дисперсии, чем В, и поэтому она хуже по данному критерию.

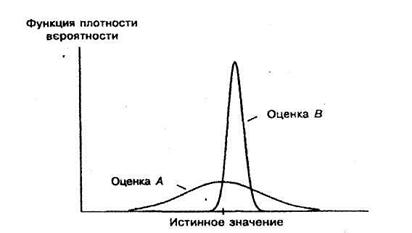
Рисунок 5.2 – Сравнение оценок

Если предел оценки по вероятности равен истинному значению характеристики генеральной совокупности, то эти оценка называется состоятельной. Иначе говоря, состоятельной называется такая оценка, которая дает точное значение для большой выборки независимо от входящих в нее конкретных наблюдений

Состоятельная оценка- оценка, у которой смещение и дисперсия стремятся к 0 при увеличении объема выборки.

Иногда бывает, что оценка, смещенная на малых выборках, является состоятельной (иногда состоятельной может быть даже оценка, не имеющая на малых выборках конечного математического ожидания). На рис. 8 показано, как при различных размерах выборки может выглядеть распределение вероятностей; Тот факт, что при увеличении размера выборки распределение становится симметричным вокруг истинного значения, указывает на асимптотическую несмещенность. То, что, в конечном счете, оно превращается в единственную точку истинного значения, говорит о состоятельности оценки.

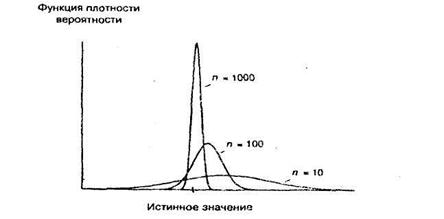
Рисунок 5.3 - Состоятельная оценка, смещенная на малых выборках

Как мы увидим далее, оценки типа показанных на рисунке 5.3, весьма важны в регрессионном анализе. Иногда невозможно найти оценку, не смещенную на малых выборках. Если при этом вы можете найти хотя бы состоятельную оценку, это может быть лучше, чем не иметь никакой оценки, особенно если вы можете предположить направление смещения на малых выборках.

Нужно, однако, иметь в виду, что состоятельная оценка в принципе может на малых выборках работать хуже, чем несостоятельная (например, иметь большую среднеквадратическую ошибку), и поэтому требуется осторожность. Подобно тому, как вы можете предпочесть смещенную оценку несмещенной, если ее дисперсия меньше, вы можете предпочесть состоятельную, но смещенную оценку несмещенной или несостоятельную оценку им обеим (также в случае меньшей дисперсии).

6 ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. ФОРМУЛИРОВАНИЕ СТАТИСТИЧЕСКИХ ГИПОТЕЗ. ОСНОВНЫЕ ПРИНЦИПЫ ПРОВЕРКИ СТАТИСТИЧЕСКИХГИПОТЕЗ

В процессе статистического анализа иногда бывает необходимо сформулировать и проверить предположения (гипотезы) относительно величины независимых параметров или закона распределения изучаемой генеральной совокупности (совокупностей). Например, исследователь выдвигает гипотезу о том, что «выборка извлечена из нормальной генеральной совокупности» или «генеральные средние двух анализируемых совокупностей равны». Такие предположения называются статистическими гипотезами.

Сопоставление высказанной гипотезы относи­тельно генеральной совокупности с имеющимися выборочными данными, сопровождаемое количе­ственной оценкой степени достоверности получа­емого вывода и осуществляемое с помощью того или иного статистического критерия, называется проверкой статистических гипотез.

Выдвинутая гипотеза называется нулевой (основной). Ее принято обозначать Н₀.

По отношению к высказанной (основной) гипотезе всегда можно сформулировать альтернативную (конкурирующую), противоречащую ей. Аль­тернативную (конкурирующую) гипотезу принято обозначать Н₁

Цель статистической проверки гипотез состоит в том, чтобы на основании выборочных данных принять решение о справедливости основной гипотезы Н_о. Если выдвигаемая гипотеза сводится к утверждению о том, что значение некоторого неизвестно­го параметра генеральной совокупности в точности равно заданной величине, то эта гипотеза называется простой, например: «Среднедушевой совокупный доход населения Казахстана составляет 3500 тг. в месяц»; «Уровень безработицы (доля безработных в численности экономически активного населения) в Казахстане равен 9%». В других случаях гипотеза называется сложной. В качестве нулевой гипотезы Н_о принято выдвигать простую гипотезу, так как обычно бывает удобнее проверять более строгое утверждение.

По своему содержанию статистические гипотезы можно подразделить на несколько основных типов:

- гипотезы о виде закона распределения исследуемой случайной величины;

- гипотезы о числовых значениях параметров исследуемой генеральной совокупности (эти гипотезы часто называют параметрическими, тогда как все остальные — непараметрическими);

- гипотезы об однородности двух или нескольких выборок или некоторых характеристик анализируемых совокупностей;

- гипотезы об общем виде модели, описывающей статистическую зависимость между признаками и др.

Так как проверка статистических гипотез осуществляется на основании выборочных данных, т. е. ограниченного ряда наблюдений, решения относительно нулевой гипотезы Н_о имеют вероятностный характер. Другими словами, такое решение неизбежно сопровождается некоторой, хотя возможно и очень малой, вероятностью ошибочного заключения как в ту, так и в другую сторону.

Так, в какой-то небольшой доле случаев a нулевая гипотеза Н_о может оказаться отвергнутой, в то время как в действительности в генеральной сово­купности она является справедливой. Такую ошибку называют ошибкой 1-го рода, а ее вероятность — уровнем значимости и обозначают a.

Наоборот, в какой-то небольшой доле случаев b нулевая гипотеза Н_о принимается, в то время как на самом деле в генеральной совокупности она ошибоч­на, а справедлива альтернативная гипотеза Н₁. Такую ошибку называют ошибкой 2-го рода. Вероятность ошибки 2-го рода обозначается как b. Вероятность 1 - b называют мощностью критерия.

При фиксированном объеме выборки можно выбрать по своему усмотрению величину вероятности только одной из ошибок a или b. Увеличение веро­ятности одной из них приводит к снижению другой. Принято задавать вероятность ошибки 1-го рода a — уровень значимости. Как правило, пользуются некоторыми стандартными значениями уровня значимости a: 0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Тогда, очевидно, из двух критериев, характеризующихся одной и той же вероятностью a (отклонить пра­вильную в действительности гипотезу Н_о), следует принять тот, которому соответствует меньшая ошибка 2-го рода b, т.е. большая мощность. Снижения вероятностей обеих ошибок a и b можно добиться путем увеличения объема выборки.

Правильное решение относительно нулевой гипотезы Н_о также может быть двух видов:

— будет принята нулевая гипотеза Н_о, когда в генеральной совокупности верна нулевая гипотеза Н_о; вероятность такого решения 1 — a;

— нулевая гипотеза Н_о будет отклонена в пользу альтернативной Н₁, когда в генеральной совокупности нулевая гипотеза Н_о отклоняется в пользу альтернативной Н₁; вероятность такого решения 1 - b —мощность критерия.

Результаты решения относительно нулевой гипотезы можно проиллюстрировать с помощью таблицы 6.1.

Проверка статистических гипотез осуществляется с помощью статистического критерия (назовем его в общем виде К), являющего функцией от результатов наблюдения.

Статистический критерий — это правило (формула), по которому определяется мера расхожде­ния результатов выборочного наблюдения с высказанной гипотезой Н_о.

Таблица 6.1 - Результаты решения относительно нулевой гипотезы Но

Нулевая гипотеза Но	Отклонена	Принята
Верна	Ошибка 1-го рода, ее вероятность a	Правильное решение, его вероятность 1-a
Неверна	Правильное решение, его вероятность 1 - b	Ошибка 2-го рода, ее вероятность b

Статистический критерий, как и всякая функция от результатов наблюдения, является случайной величиной и в предположении справедливости нулевой гипотезы Н_о подчинен некоторому хорошо изученному (и затабулированному) теоретическому закону распределения с плотностью распределения f (k).

Выбор критерия для проверки статистических гипотез может быть осуществлен на основании различных принципов. Чаще всего для этого пользуются принципом отношения правдоподобия, который позволяет построить критерий, наиболее мощный среди всех возможных критериев. Суть его сводится к выбору такого критерия К с известной функцией плотности f (k) при условии справедливости гипотезы Н_о, чтобы при заданном уровне значимости α можно было бы найти критическую точку К_кр распределения f (k), которая разделила бы область значений критерия на две части: область допустимых значений, в которой результаты выборочного наблюдения выглядят наиболее правдоподобными, и критическую область, в которой результаты выборочного наблюдения выглядят менее правдоподоб­ными в отношении нулевой гипотезы Н_о.

Если такой критерий К выбран, и известна плотность его распределения, то задача проверки статистической гипотезы сводится к тому, чтобы при заданном уровне значимости α рассчитать по выбо­рочным данным наблюдаемое значение критерия К_набл и определить, является ли оно наиболее или наименее правдоподобным в отношении нулевой гипотезы Н_о

Проверка каждого типа статистических гипотез осуществляется с помощью соответствующего кри­терия, являющегося наиболее мощным в каждом конкретном случае.

Например, проверка гипотезы о виде закона распределения случайной величины может быть осуществлена с помощью критерия согласия Пирсона χ²; проверка гипотезы о равенстве неизвестных значений дисперсий двух генеральных совокупностей — с помощью критерия Фишера F; ряд гипотез о неизвестных значениях параметров генеральных совокупностей проверяется с помощью критерия Z — нормальной распределен­ной случайной величины и критерия t-Стьюдента и т. д.

Значение критерия, рассчитываемое по специальным правилам на основании выборочных данных, называется наблюдаемым значением крите­рия (К_набл).

Значения критерия, разделяющие совокупность значений критерия на область допустимых значений (наиболее правдоподобных в отношении нулевой гипотезы Н_о) и критическую область (область значений, менее правдоподобных в отношении нулевой гипотезы Н_о), определяемые на заданном уровне значимости a по таблицам распределения случайной величины К, выбранной в качестве критерия, называются критическими точками (К).

Областью допустимых значений (областью принятия нулевой гипотезы Н_о) называют совокупность значений критерия К, при которых нулевая гипотеза Н_о не отклоняется.

Критической областью называют совокупность значений критерия К, при которых нулевая гипотеза Н_о отклоняется в пользу конкурирующей Н

Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

Если конкурирующая гипотеза — правосторонняя, например, Н₁: а > а₀, то и критическая область — правосторонняя. При правосто­ронней конкурирующей гипотезе критическая точ­ка (К) принимает положительные значения.

Если конкурирующая гипотеза — левосторонняя, например, Н₁: а< а₀, то и критическая область — левосторонняя. При левосторонней конкурирующей гипотезе критическая точка принимает отрицательные значения (К_кр.л).

Если конкурирующая гипотеза — двусторонняя, например, Н₁: а 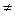а₀, то и критическая область — двусторонняя. При двусторонней конкурирующей гипотезе определяются 2 критические точки (К_кр.л и К_кр.п).

Основной принцип проверки статистических гипотез состоит в следующем:

—если наблюдаемое значение критерия (К_набл) принадлежит критической области, то нулевая гипотеза Н_о отклоняется в пользу конкурирующей Н_х;

—если наблюдаемое значение критерия (К_набл) принадлежит области допустимых значений, то нулевую гипотезу Н_о нельзя отклонить.

Можно принять решение относительно нулевой гипотезы Н_о путем сравнения наблюдаемого (К_на6л) и критического значений критерия (К_кр).

При правосторонней конкурирующей гипотезе:

- если К_набл ≤ К_кр, то нулевую гипотезу Н_о нельзя отклонить;

- если К_набл > К_кр , то нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н_1;

- При левосторонней конкурирующей гипотезе:

- если К_набл ≥ − К, то нулевую гипотезу Н₀ нельзя отклонить;

- если К_набл < − К, то нулевая гипотеза Н₀, отклоняется в пользу конкурирующей Н₁;

При двусторонней конкурирующей гипотезе:

- если -К_кр ≤ К_набл ≤ К_кр, то нулевую гипотезу Н_о нельзя отклонить;

- если К_набл > К_кр или К_набл < −К_кр, то нулевая гипотеза Н_о отклоняется в пользу конкурирующей Н_х.

Алгоритм, проверки статистических гипотез сводится к следующему:

1) сформулировать нулевую Н_о и альтернатив­ную Н₁ гипотезы;

2) выбрать уровень значимости a;

3) в соответствии с видом выдвигаемой нулевой гипотезы Н_о выбрать статистический критерий для ее проверки, т.е. — специально подобранную случайную величину К, точное или приближенное распределение которой заранее известно;

4) по таблицам распределения случайной величины К, выбранной в качестве статистического критерия, найти критическое значение К_кр (критическую точку или точки);

5) на основании выборочных данных по специ­альному алгоритму вычислить наблюдаемое значение критерия К_набл;

6) по виду конкурирующей гипотезы Н₁ определить тип критической области;

7) определить, в какую область (допустимых значений или критическую) попадает наблюдаемое значение критерия К_набл, и в зависимости от этого — принять решение относительно нулевой гипотезы Н₀

Следует заметить, что даже в том случае, если нулевую гипотезу Н_о нельзя отклонить, это не означает, что высказанное предположение о генеральной совокупности является единственно подходящим: просто ему не противоречат имеющиеся выборочные данные, однако таким же свойством наряду с высказанной могут обладать и другие гипотезы.

Можно интерпретировать результаты проверки нулевой гипотезы следующим образом:

— если в результате проверки нулевую гипотезу Н_о нельзя отклонить, то это означает, что имеющиеся выборочные данные не позволяют с достаточной уверенностью отклонить нулевую гипотезу Н_о, вероятность нулевой гипотезы Н_о больше a, а конкурирующей Н₁ — меньше 1 -a;

— если в результате проверки нулевая гипотеза Н_о отклоняется в пользу конкурирующей Н₁, то имеющиеся выборочные данные не позволяют с достаточной уверенностью принять нулевую гипотезу Н_о, вероятность нулевой гипотезы Н_о меньше a, а конкурирующей Н₁ — больше 1 - a.

7 СУЩНОСТЬ ФУНКЦИОНАЛЬНОЙ И КОРРЕЛЯЦИОННОЙ ЗАВИСИМОСТИ. ПОНЯТИЕ РЕГРЕССИИ, ВИДЫ РЕГРЕССИЙ. ЭТАПЫ РЕГРЕССИОННОГО АНАЛИЗА

Современная наука об обществе объясняет суть явлений через изучение взаимосвязей явлений. Объем продукции предприятия связан с численностью работников, стоимостью основных фондов и т. д.

Различают два типа взаимосвязей между различными явлениями и их признаками: функциональную или жестко детерминированную и статистическую или стохастически детерминированную.

Функциональная связь — это вид причинной зависимости, при которой определенному значению факторного признака соответствует одно или несколькоточнозаданных значений результативного признака.

Стохастическая связь — это вид причинной зависимости, проявляющейся не в каждом отдельном случае, а в общем, в среднем, при большом числе наблюдений. Например, изучается зависимость роста детей от роста родителей. В семьях, где родители более высокого роста, дети в среднем ниже, чем родители. И, наоборот, в семьях, где родители ниже ростом, дети в среднем выше, чем родители. Однако такого рода зависимости проявляются лишь при большом числе наблюдений.

Корреляционная связь — это неполная вероятностная зависимость между результативным и факторным признаками, которая проявляется только в массе наблюдений; каждому отдельному значению факторного признака X может соответствовать множество различных значений результативного (У).

Задачами корреляционного анализа являются:

1) изучение степени тесноты связи 2 и более явлений;

2) отбор факторов, оказывающих наиболее существенное влияние на результативный признак;

3) выявление неизвестных причинных связей.

Корреляционная связь между признаками может возникать различными путями. Важнейший путь - причинная зависимость результативного признака (его вариации) от вариации факторного признака. Например, X — балл оценки плодородия почв, У — урожайность сельскохозяйственной культуры. Здесь ясно, какой признак выступает как независимая переменная (фактор), а какой как зависимая переменная (результат).

Очень важно понимать суть изучаемой связи, поскольку корреляционная связь может возникнуть между двумя следствиями общей причины. Здесь можно привести множество примеров. Так, класси­ческим является пример, приведенный известным статистиком начала XX в. А.А.Чупровым. Если в качестве признака X взять число пожарных команд в городе, а за признак У - сумму убытков в городе от пожаров, то между признаками X и У в городах обнаружится значительная прямая корреляция. В среднем, чем больше пожарников в городе, тем боль­ше убытков от пожаров. В чем же дело? Данную корреляцию нельзя интерпретировать как связь причины и следствия, оба признака - следствия общей причины - размера города. В крупных городах больше пожарных частей, но больше и пожаров, и убытков от них за год, чем в мелких.

Корреляция возникает и в случае, когда каждый из признаков и причина, и следствие. Например, при сдельной оплате труда существует корреляция между производительностью труда и заработком. С одной стороны, чем выше производительность труда, тем выше заработок. С другой — высокий заработок сам по себе является стимулирующим фактором, заставляющим работника трудиться более интенсивно.

По направлению выделяют связь прямую и обратную, по аналитическому выражению — прямолинейную и нелинейную.

В начальной стадии анализа статистических данных не всегда требуются количественные оценки, достаточно лишь определить направление и характер связи, выявить форму воздействия одних факторов на другие.

Для представления корреляционной связи необходимо подобрать соответствующий вид регрессионного уравнения.

Регрессия (уравнение регрессии) – это математическая функция, которая наилучшим образом описывает изучаемую зависимость между показателями.

В зависимости от количества факторных признаков, включаемых в модель, различают парную (простую) и множественную регрессии:

Парная регрессия представляет собой регрессию между двумя переменным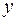и – и 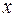, т. е. модель вида:

, (7.1)

где 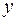– зависимая переменная (результативный признак); 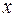– независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменным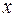и и 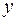нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина 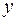складывается из двух слагаемых:

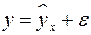, (7.2)

где 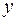– фактическое значение результативного признака; 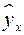– теоретическое значение результативного признака, найденное исходя из уравнения регрессии;

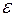– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Множественная регрессия – это уравнение связи с несколькими независимыми переменными:

y = f (x 1, x 2,..., xm) +e, (7.3)

где у – зависимая переменная (результативный признак),

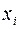– независимые, или объясняющие, переменные (признаки-факторы).

Регрессионный анализ включает ряд этапов:

1) постановка цели исследования;

2) сбор статистической информации;

3) спецификация модели - построение регрессионной модели, т. е. нахождение аналитического выражения связи;

4) расчет параметров модели

5) оценку адекватности модели, ее экономическую интерпретацию и практическое использование;

6) прогнозирование (если ставилась такая конечная цель)

8 СПЕЦИФИКАЦИЯ МОДЕЛИ, ОСНОВНЫЕ ЕЕ СПОСОБЫ

В формуле 7.2 случайная величина 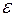называется возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака 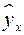, подходят к фактическим данным .

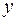К ошибкам спецификации относятся неправильный выбор той или иной математической функции для 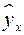и недоучет в уравнении регрессии какого-либо существенного фактора, т.е. использование парной регрессии вместо множественной.

Наряду с ошибками спецификации могут иметь место ошибки выборки, которые имеют место в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.

Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками.

Особенно велика роль ошибок измерения при исследовании на макроуровне. Так, в исследованиях спроса и потребления в качестве объясняющей переменной широко используется «доход на душу населения». Вместе с тем, статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например, в результате наличия скрытых доходов.

Предполагая, что ошибки измерения сведены к минимуму, основное внимание в статистических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции 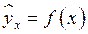может быть осуществлен тремя методами:

1) графическим;

2) аналитическим, т.е. исходя из теории изучаемой взаимосвязи;

3) экспериментальным.

При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достато

Дата добавления: 2014-01-03