Определение параметров и расчет описательной статистики множественной регрессии на компьютере

Существует большое количество пакетов прикладных программ, с помощью которых можно облегчить эконометрические расчеты. Они делятся на специализированные (Eviews, Stata, Statistica, Statgraphics) и универсальные, из которых наиболее распространен Microsoft Excel. Решение примера приведем с использованием ППП MS Excel, как наиболее доступного. Сводную таблицу основных статистических характеристик для одного или нескольких массивов данных можно получить с помощью инструмента Описательная статистика. Для этого необходимо выполнить следующие шаги: введите исходные данные, в главном меню выберите последовательно пункты Сервис/Анализ данных/Описательная статистика, после чего щелкните по кнопке ОК. Заполните диалоговое окно ввода данных и параметров вывода.

Excel предоставляет несколько функций с линейной регрессией – ЛИНЕЙН, ТЕНДЕНЦИЯ, ПРЕДСКАЗ, НАКЛОН – и две – ЛГРФПРИБЛ и РОСТ - для экспоненциальной регрессии. Эти функции вводятся в виде формулы массива и возвращают массив результатов. Каждую из этих функций можно использовать с одной или несколькими независимыми переменными. Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.

Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент Корреляция. Для этого:

1) проверьте доступ к пакету анализа. В главном меню выберите Сервис / Надстройки. Установите флажок Пакет анализа.

2) в главном меню последовательно выберите пункты Сервис / Анализ данных / Корреляция. Щелкните по кнопке ОК (рисунок 15.1):

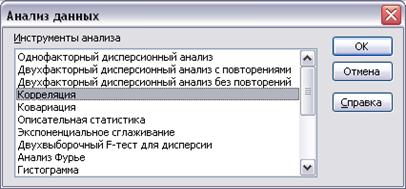
Рисунок 15.1 – Выбор инструмента Корреляция

3) заполните диалоговое окно ввода данных и параметров вывода.

Ввод данных – это весь анализируемый диапазон, включая обозначения.

Вывод – это любая пустая ячейка, начиная с которой будет выводиться результат – матрица парных коэффициентов корреляции (рисунок 15.2).

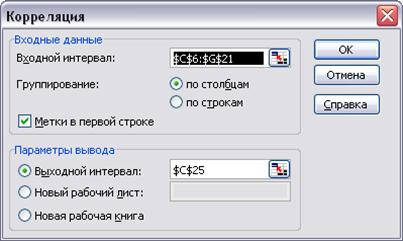
Рисунок 15.2 - Заполнение диалогового окна инструмента Корреляция

Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии у = а + bх. Порядок вычисления следующий:

1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2) выделите область пустых ячеек 5x2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1x2 – для получения только оценок коэффициентов регрессии;

3) активизируйте Мастер функций любым из способов:

а) в главном меню выберите Вставка/Функция;

б) на панели инструментов Стандартная щелкните по кнопке Вставка функции;

4) в окне Категория выберите Статистические, в окне функция - ЛИНЕЙН. Щелкните по кнопке ОК;

5) заполните аргументы функции (рисунок 15.3)

Известные значения_y - диапазон, содержащий данные результативного признака;

Известные_значения_х - диапазон, содержащий данные факторов независимого признака;

Константа - логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;

Статистика - логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.

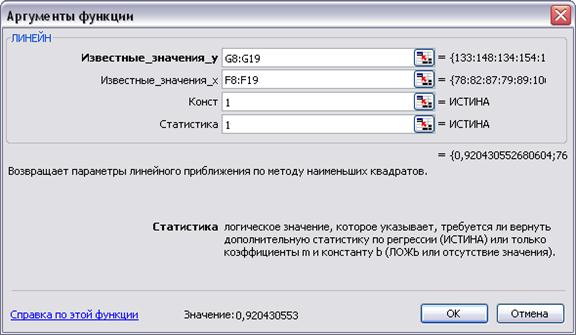
Рисунок 15.3 -Диалоговое окно ввода аргументов функции ЛИНЕЙН

6) Чтобы заполнились все элементы выходных данных, нажмите на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в таблице 15.1:

Таблица 15.1 - Регрессионная статистика

Значение коэффициента b	Значение коэффициента a
Среднеквадратическое отклонение b	Среднеквадратическое отклонение a
Коэффициент детерминации R^2	Среднеквадратическое отклонение y
F-статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Регрессионная статистика, полученная с помощью функции ЛИНЕЙН, для типовой задачи представлена на рисунке 15.4.

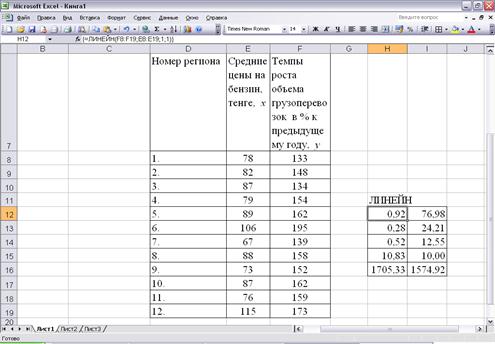
Рисунок 15.4 - Результат вычисления функции ЛИНЕЙН

Для определения теоретических значений результативного показателя при линейной регрессии используют функцию ТЕНДЕНЦИЯ. Предварительно выделив диапазон для вывода результатов находим функцию ТЕНДЕНЦИЯ, выбрав категорию Статистические. Заполняем диалоговое окно как указано на рисунке 15.5:

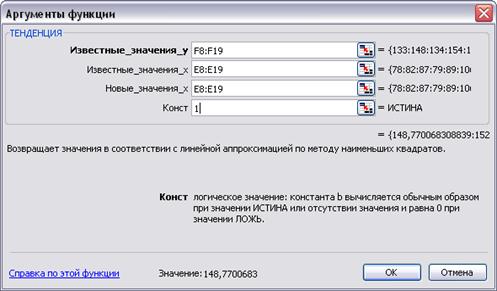
Рисунок 15.5 -Диалоговое окно ввода аргументов функции ТЕНДЕНЦИЯ

Чтобы заполнились все элементы выходных данных, нажмите на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>. Результат вычисления функции ТЕНДЕНЦИЯ представлен на рисунке 15.6:

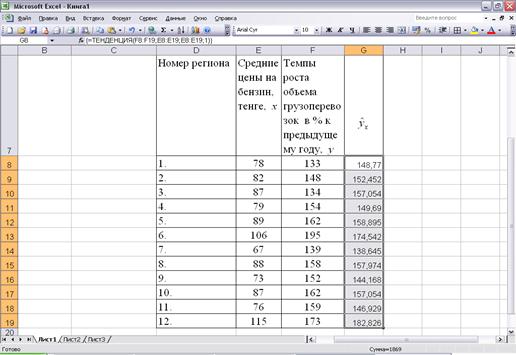
Рисунок 15.6 - Результат вычисления функции ТЕНДЕНЦИЯ

Для вычисления параметров экспоненциальной кривой 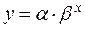в MS Excel применяется встроенная статистическая функция ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН.

При выборе оптимальной функции следует выбирать ту модель, у которой коэффициент детерминации максимальный, а остаточная дисперсия минимальна.

В рассматриваемом примере целесообразно выбрать функцию ЛИНЕЙН, поскольку с ее помощью получен более высокий коэффициент детерминации, чем с помощью функции ЛГРФПРИБЛ.

Рассчитать параметры регрессии и получить более развернутую регрессионную статистику можно вторым способом с помощью встроенного в MS Excel пакета анализа.

Если в меню Сервис еще нет команды Анализ данных, то необходимо сделать следующее: в главном меню последовательно выбираем: Сервис → Надстройки и устанавливаем «флажок» в строке Пакет анализа

Далее следуем по следующему плану.

Если исходные данные уже внесены, то выбираем Сервис→Анализ данных→Регрессия (рисунок 15.7):

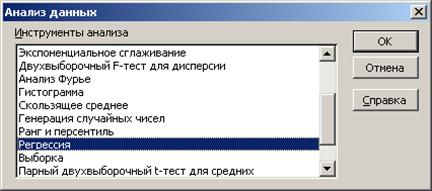
Рисунок 15.7- Выбор инструмента Регрессия

Заполняем диалоговое окно ввода данных и параметров вывода (рисунок 15.8).

Входной интервал Y – диапазон, содержащий данные результативного признака;

Входной интервал X – диапазон, содержащий данные признака-фактора;

Метки – «флажок», который указывает, содержи ли первая строка названия столбцов;

Константа – ноль – «флажок», указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист – можно указать произвольное имя нового листа (или не указывать, тогда результаты выводятся на вновь созданный лист).

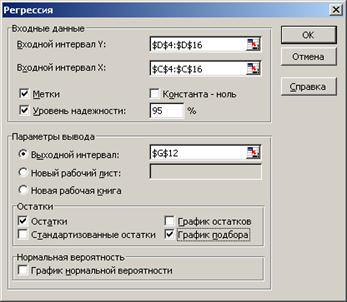
Рисунок 15.8 – Заполнение диалогового окна инструмента Регрессия

В результате использования инструмента Регрессия получаем следующие выходные данные, представленные на рисунке 15.9:

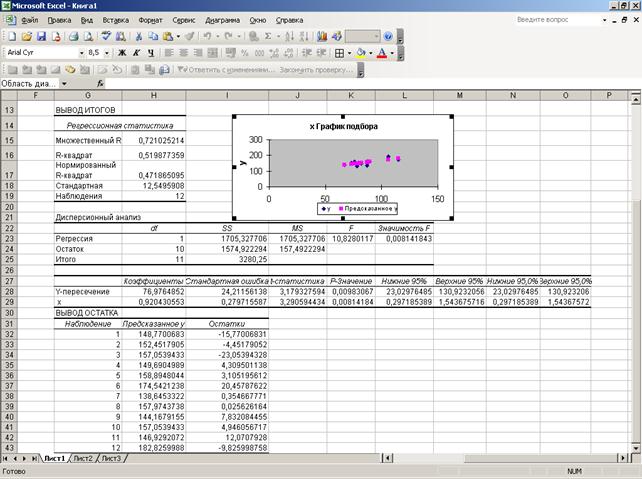
Рисунок 15.9 – Вывод итогов с помощью инструмента Регрессия

Таким образом, используя возможности прикладной программы Microsoft Excel, можно значительно облегчить эконометрические расчеты.

СПИСОК ЛИТЕРАТУРЫ

1 Айвазян С.А., Мхижарян В.С.. Прикладная статистика и основы эконометрии. М., 1998 – 235 с.

2 Венецкий И.Г., Венецкая В.И. Основные математико-статистические понятия и формулы в экономическом анализе. М.: Статистика, 1979 – 447 с.

3 Гамбаров Г.М., Журавель Н.М. и др. Статистическое моделирование и поргнозирование. Под ред. чл. Корр. АН СССР А.Г. Гранберга. – М.: Финансы и статистика, 1990, - 383 с.

4 Джонстон Дж. Эконометрические методы. Перев. с англ. – М.: Статистика, 1980, - 444 с.

5 Доугерти Кристофер. Введение в эконометрику. М.,1999 – 401 с.

6 Дюсембиев А.С. Моделирование региональных экономических систем. Автореферат канд. дисс. – Алматы, КазГАУ, 1998, - 19 с.

7 Емельянов А.С. Эконометрия и прогнозирование. М.: Экономика, 1985 – 207 с.

8 Клейнер Г.В. Производственные функции. – М.: Финансы и статистика, 1991, - 190 с.

9 Магнус Я.Р., Кактышев П.К., Пересецкий А.А. Эконометрия. Начальный курс. – М.: Дело, 1997 – 248 с.

10 Практикум по эконометрике: Учебное пособие / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2006. – 344 с.

11 Сборник задач по эконометрике: Учебное пособие для студентов экономических вузов /Сост. Е.Ю. Дорохина, Л.Ф. Преснякова, Н.П. Тихомиров. – М.: Издательство «Экзамен», 2003. – 224 с.

12 Френкель А.Н. Прогнозирование производительности труда: методы и модели. М.: Экономика, 1989 – 214 с.

13 Эконометрика: Учебник для вузов / Под ред проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА. 2002 – 311 с.

14 Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2006. – 576 с.

15 Эконометрика: Учебно-методическое пособие / Шалабанов А.К., Роганов Д.А. – Казань: ТИСБИ, 2004. – 198 с.

Дата добавления: 2014-01-03