Виды средних величин

В экономико-статистических исследованиях применяются две категории средних величин:

степенные средние;

структурные средние.

К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая и др.

К структурным средним относятся мода и медиана.

А). Средняя арифметическая простая и взвешенная.

Средняя обозначается чаще всего через 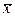. Величины, для которых вычисляется средняя, обозначается буквой .

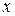Формула простой средней арифметической имеет вид:

.

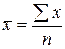Базой для вычисления простой средней арифметической служат первичные записи результатов статистического наблюдения. Числитель определяется путем простого суммирования отдельных значений признака. В знаменателе показывается численность единиц совокупности.

Например, мы имеем показатели уровня выработки рабочих одной бригады; состоящей из 10 человек

(в тыс. р.): 3,8; 4,2; 5,2; 4,2; 3,5; 4,2; 4,6; 3,8; 4,6; 5,2.

Подсчитаем среднюю выработку продукции на одного рабочего.

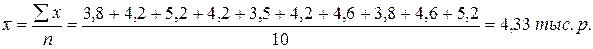
Основой для расчета средней арифметической взвешенной является обработанный материал, т.е. построенные ряды распределения.

Формула средней арифметической взвешенной имеет следующий вид:

,

где 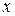– значения варианты;

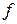– значения частот (весов);

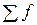– сумма всех частот (объем ряда);

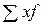– сумма произведений вариант на частоты.

Построим на основе вышеприведенных данных о выработке рабочих ряд распределения:

Таблица 5.1

Выработка продукции на одного рабочего тыс. р.	Число рабочих
3,8
4,2
5,2
3,5
4,6
Итого

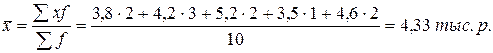
В расчете средней арифметической произведение вариант на частоты дает показатель имеющий реальный экономический смысл. Так, в рассмотренном примере произведение 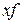– это объем продукции.

При вычислении средней арифметической взвешенной в качестве веса всегда выступает знаменатель исходного логического соотношения. Так для нашего примера, это соотношение следующее:

.

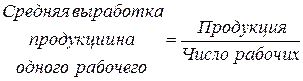Если знаменатель исходного логического соотношения известен, расчет средней величины производится по формуле средней арифметической взвешенной.

Б). Средняя гармоническая простая и взвешенная.

Наряду со средней арифметической как наиболее всеобщей формой средней, применяется в экономических расчетах и средняя гармоническая.

Средняя гармоническая – это величина обратная средней арифметической, из обратных значений признака.

Чтобы понять условия ее расчета, обратимся к примеру, приведенному в табл. 5.2.

Таблица 5.2

Цеха	Заработная плата одного рабочего, тыс. р.	Фонд заработной платы, тыс. р.
	4,6
	3,2
	2,8

Чтобы вычислить среднюю выработку продукции на одного рабочего в целом по предприятию, нужно использовать следующее исходное логическое соотношение:

.

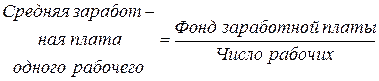Знаменатель исходного соотношения неизвестен и расчет средней производится по формуле средней гармонической взвешенной:

.

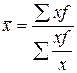В этой формуле 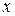– варианты (для нашего примера уровни заработной платы одного рабочего).

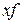– произведения вариант на частоты (в нашем случае фонд зарплаты).

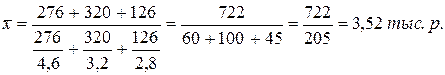
Как мы видим, из расчета среднюю гармоническую взвешенную применяют тогда, когда необходимые веса (частоты) в исходных данных не заданы непосредственно, а входят сомножителем в один из имеющихся показателей, выступающий так называемыми "мнимыми весами".

Среднюю гармоническую в расчетах можно заменить средней арифметической, достаточно лишь предварительно вычислить веса. В нашем примере можно было предварительно по каждому цеху вычислить число рабочих.

То есть, средняя гармоническая в статистике есть преобразованная средняя арифметическая, которая применяется тогда, когда неизвестны частоты ряда распределения.

Средняя гармоническая простая вычисляется по формуле:

,

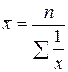где 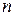– число вариант.

Эту формулу целесообразно применять вместо средней гармонической взвешенной в том случае, если объем явлений (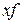) равны у всех единиц совокупности.

Таблица 5.3

Рынки	Цена за единицу р.	Товарооборот тыс. р.
	12,5	2 700
	10,8	2 700

Определим среднюю цену за единицу по двум рынкам.

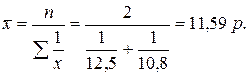
В). Другие виды степенных средних.

В зависимости от исходной информации, цели исследования кроме средней арифметической и средней гармонической могут применяться и другие виды степенных средних, формулы их расчета приведены в табл. 5.4.

Таблица 5.4

Наименование	Формулы средней
простая	взвешенная
Средняя геометрическая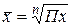
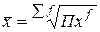
Средняя квадратическая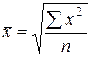
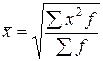
Средняя кубическая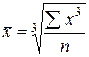
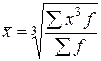
Средняя биквадратическая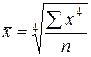

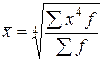
Использование формул средней геометрической в практических расчетах будет рассмотрено нами в теме "Ряды динамики", заметим лишь, что наибольшее применение имеет первая формула.

Остальные виды средних, приведенных в таблице, практически в экономических расчетах не применяются, чаще в технических, но средняя квадратическая; например используется для измерения колеблемости признака.

Степенные средние различных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения. И чем выше показатель степени, тем больше и величина соответствующей средней:

.

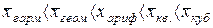Эта связь средних в статистике называется правилом мажорантности средних.

Дата добавления: 2014-01-03