Расчет средней арифметической из интервального ряда распределения

Средняя величина из интервального вариационного ряда распределения определяется по формуле средней арифметической взвешенной. За значение x берется середина каждого интервала, которую вычисляют как величину арифметическую простую, исходя из верхней и нижней границы каждого интервал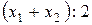а: . За 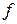принимается частота каждого интервала.

Например, вычислим средний стаж работы 1 рабочего на предприятии по данным табл. 5.5.

Таблица 5.5

Стаж работы лет	Число рабочих	Расчет середины интервала х
до 5		(0+5):2=2,5
5-10		(5+10):2=7,5
10-15		(10+15):2=12,5
15-20		(15+20):2=17,5
20 и выше		(20+25):2=22,5
Итого

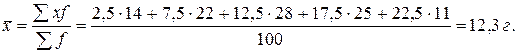
Средний стаж работы одного рабочего на предприятии составляет 12,3 года.

Средняя величина, полученная из интервального ряда всегда менее точна, чем средняя, полученная из дискретного ряда распределения. Это объясняется тем, что за варианты берется середина интервала каждой группы, исходя из предположения равномерности распределения вариант в интервале. Практически же такая равномерность отсутствует, средняя в каждой группе может не совпадать с серединой интервала.

Хотя, несмотря на довольно значительные ошибки по группам, на среднем итоге они сказываются в меньшей степени.

Степень расхождения между средней из дискретного и интервального ряда зависит от определенных причин.

Первой причиной является число частот в каждой группе. Чем больше частота тем вероятнее, что середина интервала будет незначительно отличаться от групповой средней.

Второй причиной является величина интервала. Чем меньше величина интервала, тем меньше середина интервала отличается от групповой средней.

Третьей причиной является характер распределения. Чем симметричнее распределение, тем меньше ошибка, возникающая при использовании середин интервалов.

Четвертой причиной является принцип построения интервального ряда. При равных интервалах центр его будет ближе примыкать к средней арифметической по данной группе. Если же интервалы неравные и по размеру резко отличаются друг от друга, то расхождения между средней и серединой интервала может быть значительным.

Дата добавления: 2014-01-03