Виды дисперсий и правило их сложения. Разделив изучаемую совокупность на качественно однородные группы, можно исчислить для каждой из групп среднюю и дисперсию

Разделив изучаемую совокупность на качественно однородные группы, можно исчислить для каждой из групп среднюю и дисперсию.

Групповая средняя говорит о среднем размере изучаемого признака данной группы единиц.

Групповая дисперсия характеризует средний квадрат отклонения индивидуальных значений данного признака от групповой средней.

Рассчитаем эти показатели по следующим данным:

Таблица 6.3

Урожайность картофеля по участкам

Урожайность, в ц с 1 га	Участки, га
Всего	в том числе
удобренные	неудобренные
до 100		–
100-120
120-140
140 и выше			–
Итого

Определим групповые средние 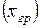по формуле:

,

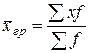где 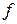– численность вариант в каждой группе.

Средняя урожайность картофеля на удобренных участках:

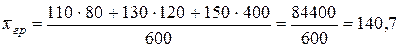ц.

Средняя урожайность на неудобренных участках:

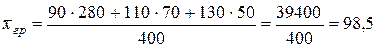ц.

Исчислим групповые дисперсии:

.

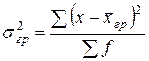Дисперсия урожайности на удобренных участках:

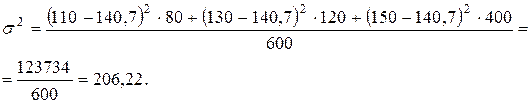
Дисперсия урожайности на неудобренных участках:

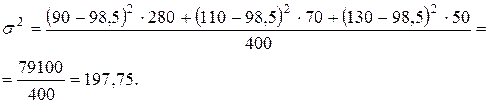
Можно рассматривать всю совокупность как единое целое, не подразделяя ее на группы и тоже исчислить общую среднюю и общую дисперсию.

Общая средняя характеризует средний размер признака в данной совокупности в целом.

Общая дисперсия показывает средний квадрат отклонений индивидуальных значений от общей (генеральной) средней.

Рассчитаем общую среднюю по формуле:

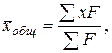
где 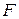– численность всей совокупности.

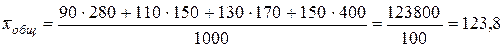ц.

Общая дисперсия:

.

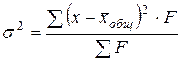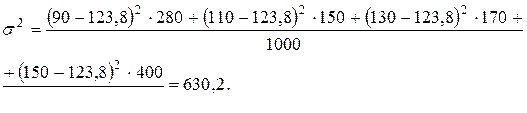
Между групповой и общей средней можно исчислить показатель вариации, где групповые средние рассматриваются как индивидуальные значения совокупности, это межгрупповая дисперсия:

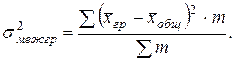
Межгрупповая дисперсия служит мерой колеблемости частных (групповых) средних около общей средней. Величина межгрупповой дисперсии указывает насколько частные совокупности однороднее общей.

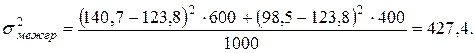
Таким образом получается три вида дисперсий: общая, групповая и межгрупповая. Все эти дисперсии взаимосвязаны между собой следующим образом: величина общей дисперсии равна сумме межгрупповой дисперсии и средней дисперсии из групповых.

Средняя дисперсия из групповых вычисляется как средняя взвешенная величина, в качестве веса берется численность каждой группы ():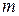

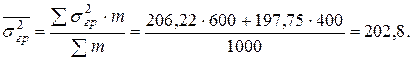
Проверим взаимосвязь дисперсий, которую в математике называют теоремой или правилом сложения дисперсий:

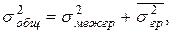
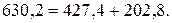
Общая дисперсия отражает вариацию результативного признака, вызванную воздействием всей совокупности факторов. В нашем примере она показывает вариацию урожайности на всем массиве под влиянием всех совместно действующих факторов: внесения удобрений, погодных условий, организации работ и т.д.

Межгрупповая дисперсия характеризует вариацию результативного признака, которая происходит под влиянием фактора положенного в основу группировки. Она характеризует колеблемость урожайности под влиянием одного фактора – внесенных удобрений.

Внутригрупповая дисперсия характеризует случайную вариацию. Эта вариация возникает под влиянием других, неучитываемых факторов и не зависит от признака – фактора, положенного в основу группировки.

Дата добавления: 2014-01-03