Вопрос 4.6. Выбор численных значений допусков формы и расположения

И расположения поверхностей

Условные обозначения допусков формы

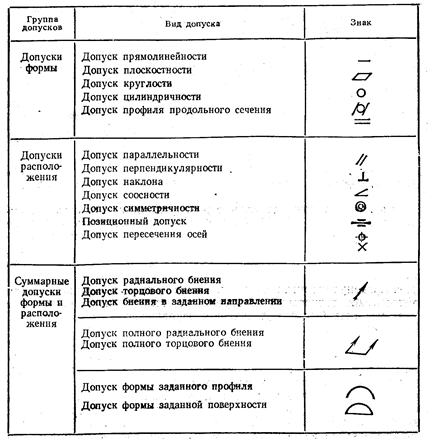
Стандартизация числовых значений допусков формы и расположения поверхностей позволяет унифицировать технические требования к изделиям, повысить их взаимозаменяемость. Преимущества стандартизации заключается также в том, что допуски взаимоувязываются с номинальными размерами и допусками размеров по квалитетам.

Стандартами установлены 16 степеней точности допусков формы и расположения. Области применения примерно одинаковы с квалитетами точности размеров. Численные значения допусков формы выбираются по методу аналогов из справочной литературы. Например, 1-2 степени точности допусков плоскостности и прямолинейности применяется для измерительных и рабочих поверхностей особо точных средств измерений (концевые меры длины, направляющие прецизионных шлифовальных станков). Для всех случаев отклонений формы численное значение допуска формы должно ограничиваться допуском на размер:

Т_ф ≤ Т_разм.

Допуски формы назначаются для тех случаев, когда отклонение формы оказывает влияние на работоспособность и качество изделия. Так, для поверхностей, сопрягаемых с кольцами подшипников качения, допуски круглости должны составлять менее 25% допуска на размер. В зависимости от соотношения между допусков размера и допусками формы и расположения устанавливаются уровни относительной геометрической точности: А – нормальная относительная геометрическая точность (допуск формы в среднем составляет 60% от допуска размера); В – повышенная относительная геометрическая точность (40%); С – высокая, для которой допуск формы составляет в среднем 25%. Стандартами рекомендовано назначение степеней точности в зависимости от уровней относительной геометрической точности и квалитета допуска размера. Если на чертеже численное значение допуска не указано, то, автоматически, численное значение допуска формы ограничивается допуском на размер.

Численное значение допусков расположения также можно выбрать по методу аналогов и примерам назначения допусков расположения в справочной литературе. Так, для вращающихся валов допуск соосности поверхностей, сопрягаемых с подшипниками качения рекомендуется принимать по эмпирической формуле Т= 48/ n, где n – частота вращения вала.

Для определения численных значений допусков расположения используется и расчетный метод, основанный на теории размерных цепей.

В отличие от отклонений формы, отклонения расположения не выявляются при контроле точности размеров и численные значения допусков расположения (кроме допусков параллельности) могут превышать допуски на размер.

Дата добавления: 2014-01-03