Комплексные числа

Комплексным числом z называется число вида

z = x + iy, (1)

где x и y — вещественные числа, i — мнимая единица (i ²=—1). Число x называется вещественной частью комплексного числа z. Символически это записывается в виде x = Rez. Число у называется мнимой частью z (записывается: y = lmz). Число

z *= x — iy. (2)

называется комплексно сопряженным числу x + iy. Вещественному числу x можно сопоставить точку на оси x.

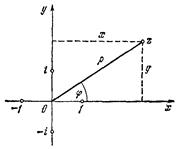Комплексному числу z можно сопоставить точку на плоскости, имеющую координаты x, y (рис.). Каждая точка плоскости определяет некоторое комплексное число z. Следовательно, комплексное число можно задать с помощью декартовых координат x и y соответствующей точки. Однако то же самое число можно задать с помощью полярных координат ρ и φ. Между обеими парами координат имеются соотношения

x = ρ∙ cos φ, y = ρ∙ sin φ, 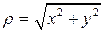, φ= arctg (y / x). (3)

Расстояние от начала координат до точки, изображающей число z, называется модулем комплексного числа (обозначается | z |). Очевидно, что

z=.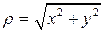

Число φ называют аргументом комплексного числа z.

Приняв во внимание соотношения (3), можно представить комплексное число в тригонометрической форме:

z =ρ(cos φ+ i sin φ).

Два комплексных числа z ₁= x ₁+ iy ₁ и z ₂= x ₂+ iy ₂ считаются равными друг другу, если в отдельности равны их вещественные и мнимые части:

z ₁= z ₂, если x ₁= x ₂ и y ₁= y ₂.

Модули двух равных между собой комплексных чисел одинаковы, а аргументы могут отличаться лишь слагаемым, кратным 2π:

ρ₁ = ρ₂, φ₁=φ₂±2kπ.

Из выражений (1) и (2) видно, что в случае, когда z *= z, мнимая часть z есть нуль, т. е. число z оказывается чисто вещественным. Таким образом, условие вещественности числа z можно записать в виде

z * = z.

В математике доказывается соотношение

e^{i φ} = со s φ + isin φ, (4)

которое называется формулой Эйлера. Заменив в этой формуле φ на —φ и учтя, что cos (—φ)= cos φ, a sin (‑φ) = — sin φ, получим соотношение

e ^{‑ i φ} = со s φ ‑ i ∙ sin φ. (5)

Сложим выражения (4) и (5) и решим получившееся соотношение относительно cosφ. В результате имеем

со s φ = 1/2∙(e^{i φ} +е^{‑ i φ}).

Вычтя (5) из (4), получим, что sin φ = (1/2 i) (e^{i φ} ‑ e ^{‑ i φ}).

С помощью формулы (4) комплексное число можно записать в показательной форме:

z = ρ e ^{‑ i φ}.

Комплексно сопряженное число в показательной форме имеет вид

z * = ρ e ^{‑ i φ}.

При сложении комплексных чисел складываются отдельно их вещественные и мнимые части:

z ₁+ z ₂=(x ₁+ x ₂)+ i (y ₁+ y ₂).

Перемножение комплексных чисел удобно осуществлять, беря эти числа в показательной форме:

z = z ₁∙ z ₂ = ρ₁ e^{i φ}₁∙ρ₂ e^{i φ}₂ = ρ₁ρ₂ e^{i (φ}₁ ^{+ φ}₂⁾

Модули комплексных чисел перемножаются, а аргументы складываются:

ρ=ρ₁∙ρ₂, φ=φ₁+φ₂.

Аналогично осуществляется деление комплексных чисел:

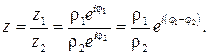
легко получить, что

z ∙ z * = ρ².

(квадрат модуля комплексного числа равен произведению этого числа на его комплексно сопряженное).

Дата добавления: 2014-01-03