Множественная корреляция. Лекция 9. Множественная линейная регрессия

Лекция 9. Множественная линейная регрессия. Оценка значимости

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

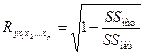(3.1)

где S S _ост – остаточная сумма квадратов для уравнения y = f (x ₁, x ₂,…, x_p); S S_общ – общая сумма квадратов результативного признака.

Методика построения индекса множественной корреляции аналогична построению индекса корреляции для парной зависимости. Границы его изменения те же: от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:

.

При правильном включении факторов в регрессионный анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем и четвертом знаках). Сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение того или иного фактора. Так, если y рассматривается как функция x и z и получен индекс множественной корреляции R_yzx = 0,85, а индексы парной корреляции при этом были R_yx = 0,82 и R_yz = 0,75, то совершенно ясно, что уравнение парной регрессии y = f (x) охватывало 67,2 % колеблемости результативного признака под влиянием фактора x, а дополнительное включение в анализ фактора z увеличило долю объясненной вариации до 72,3 %, т.е. уменьшилась доля остаточной вариации на 5,1 % (с 32,8 % до 27,7 %).

В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная сумма квадратов, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений п. Если число параметров при x_j равно т и приближается к объему наблюдений, то остаточная сумма квадратов будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, применяется скорректированный (нормированный) индекс (коэффициент) множественной корреляции

Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов делится на число степеней свободы остаточной вариации (п – т), а общая сумма квадратов отклонений – на число степеней свободы в целом по совокупности (п – 1).

Формула скорректированного индекса множественной детерминации имеет вид:

, (3.3)

где п – число наблюдений; т – число параметров при переменных

Чем больше величина т, тем сильнее различия и R ².

Для линейной зависимости признаков скорректированный коэффициент множественной корреляции определяется по той же формуле, что и индекс множественной корреляции, т.е. как корень квадратный из .

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F -критерия Фишера:

(3.5)

где s ²_факт – факторная дисперсия на одну степень свободы; R ² – коэффициент (индекс) множественной детерминации; n – число наблюдений; m – число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов); s ²_ост – остаточная дисперсия на одну степень свободы.

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -отношения, т.е. критерий F:

.

При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:

(3.8)

где b_xi – стандартизованные коэффициенты регрессии; r_yxi – парные коэффициенты корреляции результата с каждым фактором.

Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции или совокупного коэффициента корреляции.

Дата добавления: 2014-01-03