Частные уравнения регрессии

На основе линейного уравнения множественной регрессии

y = a + b ₁ × x ₁ + b ₂ × x ₂ + … + b_k × x_k + e

могут быть найдены частные уравнения регрессии:

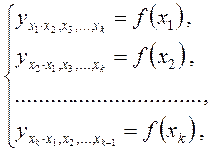
т.е. уравнения регрессии, которые связывают результативный признак с соответствующими факторами x при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Частные уравнения регрессии имеют следующий вид:

;

;

…………………………………………………………;

.

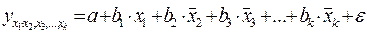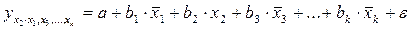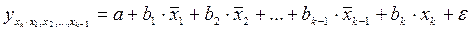При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем:

;

;

…………………………;

,

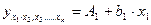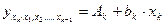где

;

;

…………………………………;

.

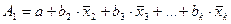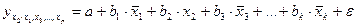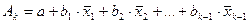В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:

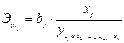(3.5)

где b_j – коэффициенты регрессии для фактора x_j в уравнении множественной регрессии; 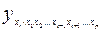– частное уравнение регрессии.

На основе данной информации могут быть найдены средние по совокупности показатели эластичности:

.

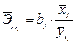Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

Наряду со средними показателями эластичности в целом по совокупности предприятий на основе частных уравнений регрессии могут быть определены частные коэффициенты эластичности для каждого предприятия.

Пример: пусть имеем следующее уравнение регрессии:

y = –4,874 + 0,585 × x ₁ + 0,240 × x ₂.

При этом средние значения для рассматриваемых признаков составили:

y = 5; x ₁ =14; x ₂ = 7.

Частные уравнения регрессии составят:

,

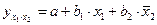т.е. ;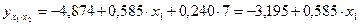

,

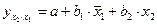т.е. .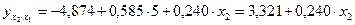

Подставив в данные уравнения фактические значения соответствующих факторов по отдельным предприятиям, получим значения моделируемого показателя y при заданном уровне одного фактора и средних значениях других факторов, представленные в следующей таблице:

№ п/п	y	x1	x2
				3,243902	4,04065
				2,658537	3,800813
				3,829268	4,280488
				7,341463	5,719512
				5,585366	5,95935
				4,414634	4,760163
				4,414634	4,520325
				5,585366
				6,170732	5,719512
				6,756098	6,199187

Эти расчетные значения результативного признака используются для определения частных коэффициентов эластичности по приведенной выше формуле. Так, если в регионе x ₁ = 11; x ₂ = 3, то частные коэффициенты эластичности составят:

;

;

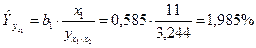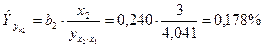Как видим, частные коэффициенты эластичности для предприятия несколько отличаются от аналогичных средних показателей по совокупности предприятий. Они могут быть использованы при принятии решений по развитию конкретных предприятий.

Дата добавления: 2014-01-03