Динамики

Для вышеназванных показателей могут быть рассчитаны обобщающие показатели в виде средних величин. Использование средних показателей порой становится просто необходимым. Например, сельскохозяйственная продукция в огромной степени зависит от погодных условий данного года и сравнение годовых показателей становится нецелесообразным. Правильнее сравнивать среднегодовые приросты и темпы роста за определенные промежутки времени.

1. Средний уровень ряда называется также хронологической средней или временной средней. Средний уровень ряда рассчитывается по-разному для моментных и интервальных рядов динамики.

Чтобы найти средний уровень интервального ряда, достаточно сумму уровней этого ряда разделить на число периодов, к которым она относится, т.е.

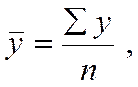
где å у - сумма уровней ряда;

n - число уровней ряда.

Следовательно, средняя хронологическая интервального ряда динамики вычисляется по формуле средней арифметической простой.

Если отдельные периоды интервального ряда динамики имеют неодинаковую длину, то для определения среднего уровня следует воспользоваться средней арифметической взвешенной, т.е. рассчитать его, взвешивая уровни по числу равных периодов.

Cредний уровень моментного ряда динамики так исчислять нельзя.

Для моментных рядов динамики при неполных уровнях применяется взвешивание сумм каждой смежной пары уровней по продолжительности периода между ними, т.е.

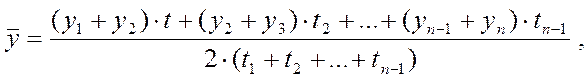
где: t1 - время (в соответствующих единицах) между моментом регистрации у1 и моментом регистрации у2;

t2 - время между моментом регистрации у2 и у3 и т.д.

В знаменателе берется удвоенная сумма периодов, поскольку каждое слагаемое числителя суммируется два раза.

С помощью метода математической индукции, для «n» уровней формула среднего уровня моментного ряда записывается:

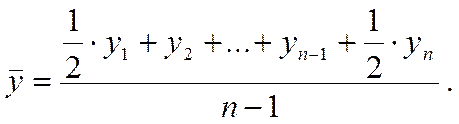
2. Средний абсолютный прирост - это средняя из абсолютных приростов за равные промежутки времени одного периода.

Обычно расчет среднего абсолютного прироста производят по цепным абсолютным приростам D уц по формуле:

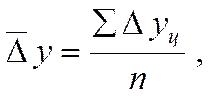
где: 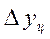- абсолютный прирост (цепной);

n - число абсолютных приростов за

период.

Средний абсолютный прирост можно исчислить и непосредственно по абсолютным уровням ряда динамики «у» по формуле:

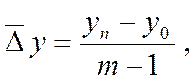
где m - число учетных единиц времени в ряду динамики.

В тех случаях, когда в качестве исходных материалов даны накопленные (базисные) абсолютные приросты Dуб, и основываясь на взаимосвязи между цепными и базисными абсолютными приростами, расчет среднего абсолютного прироста производится по формуле:

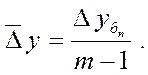
3. При исчислении среднего темпа роста нужно учитывать, что скорость развития явлений идет по правилам сложных %, где накапливается прирост на прирост. Поэтому средний темп роста принято вычислять по формуле средней геометрической из темпов роста за составляющие период промежутки времени. Применительно к рядам динамики формула средней геометрической в общем виде записывается так:

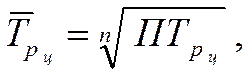
где: 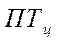- произведение цепных темпов

роста (в коэффициентах);

n - число темпов.

Основные методы определения средних темпов динамики:

1). Исчисление среднего темпа по цепным темпам роста:

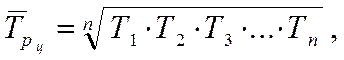
где Тц - цепные темпы роста (в

коэффициентах);

n - число темпов.

2). Расчет среднего темпа динамики по базисным темпам роста:

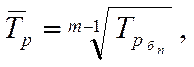
где Тб - базисный темп роста (в

коэффициентах);

m - число учетных единиц времени

в изучаемом периоде.

3). Расчет среднего темпа роста по абсолютным уровням ряда динамики:

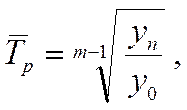
где уn - конечный уровень ряда динамики;

уо - базисный уровень ряда динамики;

m - число учетных единиц времени в изучаемом периоде.

4. Среднегодовой темп прироста вычисляется на основе данных среднегодового темпа роста:

V. Методы выявления в рядах динамики основной тенденции развития

Важным направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей тенденции развития (тренда). Это осуществляется с использованием специальных методов анализа рядов динамики. Конкретное их использование зависит от характера исходной информации и задач анализа.

Изменения уровней рядов динамики обусловлены влиянием на изучаемое явление ряда факторов, которые неоднородны по силе, направлению и времени их воздействия. Постоянно действующие факторы оказывают определяющее влияние и формируют в рядах динамики основную тенденцию развития (тренд). Воздействие других факторов проявляется периодически. Это вызывает повторяемые во времени колебания уровней рядов динамики. Действие разовых (спорадических) факторов отображается случайными (кратковременными) изменениями уровней рядов динамики.

Различные результаты действия постоянных, периодических и разовых причин и факторов на уровни развития социально-экономических явлений во времени обусловливают необходимость изучения основных компонентов рядов динамики:

1. тренда;

2. периодических колебаний;

3. случайных отклонений.

Особенностью изучения рядов динамики является то, что основная тенденция роста в одних рядах проявляется при визуальном обзоре исходной информации, а в других рядах динамики она не проявляется и может быть выражена расчетным путем в виде некоторого теоретического уровня.

Потребности квалифицированного управления предприятием, прогностические и другие цели обусловливают необходимость придания основной тенденции развития обобщающей количественной оценки.

Наиболее распространенными методами статистического изучения тренда являются:

1. Укрупнение интервалов.

2. Сглаживание скользящей средней.

3. Аналитическое выравнивание.

1. Метод укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, скрывающих основную тенденцию развития. Основа метода заключается в преобразовании первоначального ряда динамики в ряды более продолжительных периодов (месячные в квартальные, квартальные в годовые и т.д.).

2. Сглаживание методом скользящей средней предусматривает определение по исходным уровням (эмпирическим данным) расчетных (теоретических) уровней. При этом путем осреднения эмпирических данных индивидуальные колебания погашаются, а основная тенденция развития выражается в виде некоторой плавной линии.

Основное условие применения этого метода состоит в вычислении звеньев подвижной (скользящей) средней из такого число уровней ряда, которое соответствует длительности наблюдаемых в ряду динамики циклов.

Например, для ряда динамики, отображающего развитие явления по кварталам, скользящие средние обычно составляются из четырехчленных звеньев. Их расчет состоит в определении средних величин из четырех уровней ряда с отбрасыванием при вычислении каждой новой скользящей средней одного уровня слева и присоединением одного уровня справа:

Первая средняя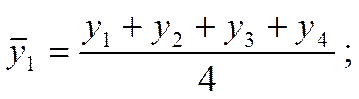

Вторая средняя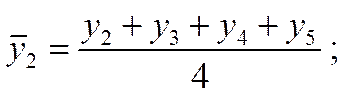

Третья средняя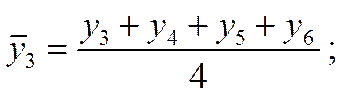

и т.д.

Для четного числа уровней каждое значение скользящей средней приходится на промежуток между двумя смежными кварталами. Так, первая скользящая средняя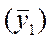записывается между II и III кварталами, вторая 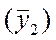- между III и IV кварталами. Для определения сглаженных уровней производится центрирование 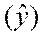. Для III квартала определяется серединное значение между первой и второй скользящими средними, для IV квартала центрируются вторая и третья скользящие средние. Полученные значения сглаженных уровней изображаются на графике, где проявляется основная тенденция развития явления.

При применении метода скользящей средней в ряду динамики месячных уровней рассчитываются 12-членные скользящие средние:

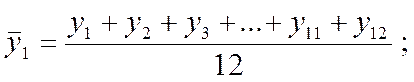
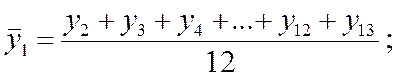
и т.д. с последующим центрированием полученных значений.

Если при сглаживании рядов динамики звенья скользящей средней составляются из нечетного числа уровней, то необходимость в центрировании отпадает.

Применение в анализе рядов динамики двух вышеперечисленных методов позволяет выявить тренд для его описания, но получать обобщенную статистическую оценку тренда посредством этих методов невозможно. Измерение тренда может быть достигнуто методом аналитического выравнивания.

4. Метод аналитического выравнивания.

При этом методе уровни ряда динамики выражаются в виде функции времени:

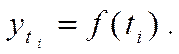
При теоретическом анализе выявляется характер развития явления во времени и на этой основе выбирается то или иное математическое выражение типа изменения явления, т.е. определяется адекватная математическая функция.

Подбор адекватной функции осуществляется методом наименьших квадратов, т.е. минимальностью отклонений суммы квадратов между теоретическими 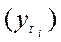и эмпирическими 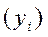уровнями:

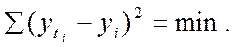
Это является критерием оценки соответствия теоретических уровней с эмпирическими уровнями ряда динамики.

Одним из условий обоснованного применения метода аналитического выравнивания является знание типов развития социально-экономических явлений во времени:

1) равномерное развитие. Для этого типа динамики соответствуют постоянные абсолютные приросты:

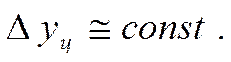
Основная тенденция развития в рядах динамики со стабильными абсолютными приростами отображается уравнением прямолинейной функции:

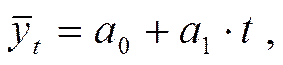
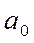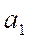где и - параметры уравнения;

t - обозначения времени.

Параметр 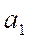является коэффициентом регрессии, определяющим направление развития. Если 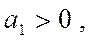то уровни ряда динамики равномерно возрастают, а при 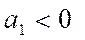происходит их равномерное снижение;

2) равноускоренное (равнозамедленное) развитие. Данному типу свойственно постоянное во времени увеличение или замедление развития. Уровни таких рядов динамики изменяются с постоянными темпами прироста:

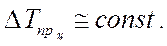
Основная тенденция развития в рядах динамики со стабильными темпами прироста отображается функцией параболы второго порядка:

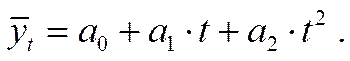
Параметр 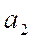характеризует постоянное изменение интенсивности развития (в единицу времени). При 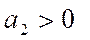происходит ускорение развития, а при 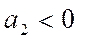идет процесс замедления роста. Параметр 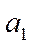может быть как со знаком плюс, так и со знаком минус.

3) развитие с переменным ускорением (замедлением). Для данного типа динамики основная тенденция развития выражается функцией параболы третьего порядка:

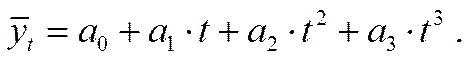
Параметр 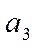отображает изменение ускорения. При 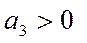ускорение возрастает, а при 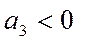ускорение замедляется.

4) развитие по экспоненте. Данный тип динамики характеризуют стабильные темпы роста:

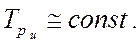
Основная тенденция в рядах динамики с постоянными темпами роста отображается показательной функцией:

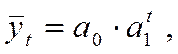
где 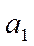- темп роста (снижения) изучаемого явления в единицу времени, т.е.интенсивность развития.

5) развитие с замедлением роста в конце периода. У этого типа динамики показание цепного абсолютного прироста сокращается в конечных уровнях ряда динамики:

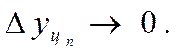
Основная тенденция развития в таких рядах динамики выражается полулогарифмической функцией:

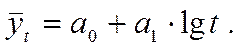
При аналитическом выравнивании в рядах динамики можно применить и другие математические функции. Так, при изучении основной тенденции неудовлетворенного и реализованного спроса населения применяются:

степенная функция -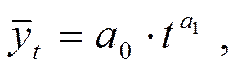

функция гиперболы -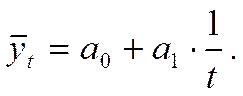

Логистическая форма тренда имеет вид кривой, похожей на латинскую букву s положенной на бок. Ввиду этого ее также называют эсообразной кривой. Она имеет два перегиба, для которых характерны ускоряющийся рост к равномерному развитию (вогнутость) и от равномерного роста посреди периода к замедляющемуся процессу (выпуклость). Логистическая форма тренда выражается формулой:

,

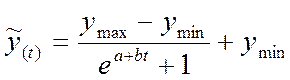где е - основание натуральных алгоритмов;

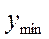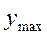и - минимальное и максимальное из возможных значений уровня;

а и в - параметры тренда.

Данная функция может быть использована для отображения развития явления в течение длительного периода времени, проходящего все фазы своего развития. Например, процесса насыщения демографической группы потребителей определенным видом товара, сначала медленный, но все более ускоряющийся рост доли семей, имеющих этот товар, затем рост равномерный, потом он замедляется при приближении к 100 %.

При условии, если 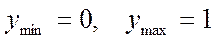или 100 %, то уравнение логистической формы тренда принимает вид:

.

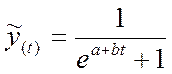Рассмотрим как производится выравнивание ряда динамики по прямой линии:

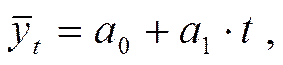
где 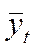- значения уровней выравненного ряда, которое нужно вычислить;

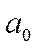и 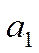- параметры прямой;

t - показатели времени (дни, месяцы, годы и т.д.

Для вычисления параметров функции на основе требований метода наименьших квадратов составляется система нормальных уравнений:

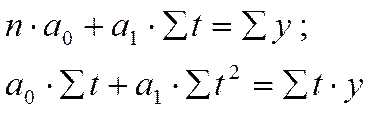
Для решения системы уравнений обычно применяется способ определителей, позволяющий получать более точные результаты за счет сведения к минимуму ошибки из-за округлений в расчетах параметров:

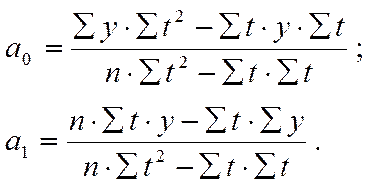
По вычисленным параметрам производится синтезирование трендовой модели функции.

На основе модели определяются теоретические уровни тренда 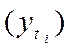для каждого года анализируемого ряда динамики. Правильность расчетов проверяется по равенству:

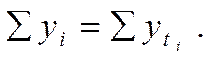
При изучении социально-экономических явлений приходится иметь дело со сложным механизмом взаимодействия факторов, формирующих тренд. Поэтому не всегда можно получить надежные выводы о типе и виде математической функции. В лучшем случае может быть выдвинута рабочая гипотеза о возможных типах развития. Но выбор на этой основе конкретной математической функции очень затруднителен, особенно если развитие идет по криволинейным функциям.

Для подтверждения гипотезы о возможном типе развития можно использовать графический метод. Наглядное изображение позволяет получать образное представление о размещении на поле графика эмпирических уровней. Однако дать обобщенную статистическую характеристику тренда графический метод не может.

Одним из используемых в практике изучения тренда показателей адекватности математической функции является стандартизованная ошибка аппроксимации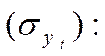

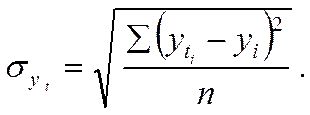
Применение данной формулы основано на том, что за наиболее адекватную принимается функция, у которой стандартизованная ошибка аппроксимации минимальная.

Для определения параметров математических функций при анализе тренда в рядах динамики используется способ отсчета времени от условного начала. Он основан на обозначении в ряду динамики показаний времени таким образом, чтобы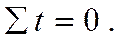

При этом в ряду динамики с нечетным числом уровней порядковый номер уровня, находящегося в середине ряда, обозначают через нулевое значение и принимают за условное начало отсчета времени с интервалом (+1) всех последующих уровней и (-1) всех предыдущих уровней.

Например, при n = 5 обозначения времени будут следующими: - 2, - 1, 0, + 1, + 2. При четном числе уровней, например, n = 6 порядковые номера верхней половины ряда (от середины) обозначаются числами: - 1, - 3, - 5, а нижней половины ряда обозначаются: + 1, + 3, +5.

При использовании способа условного обозначения времени, когда 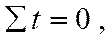параметры математических функций определяются по формулам:

А) для прямолинейной функции

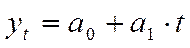
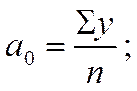
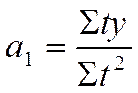
б) для параболы второго порядка

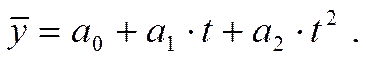
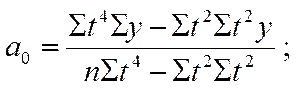
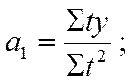
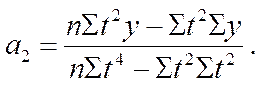
в) для параболы 3-го порядка

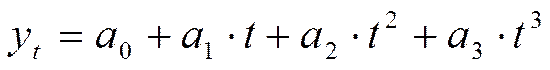
параметры рассчитываются по формулам:

.

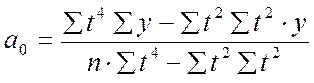
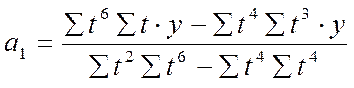
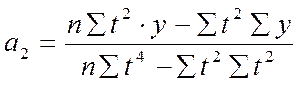
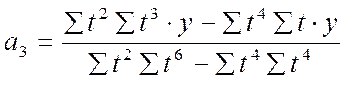VI. Изучение сезонных колебаний

Под сезонными колебаниями понимаются более или менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений. Проявляются они с различной интенсивностью во всех сферах жизни общества: производстве, обращении и потреблении.

При статистическом изучении в рядах внутригодовой динамики сезонных колебаний решаются следующие две взаимосвязанные задачи:

1. выявление специфики развития изучаемого явления во внутригодовой динамике;

2. измерение сезонных колебаний изучаемого явления с построением модели сезонной волны.

Дата добавления: 2014-01-03