Процентные ставки и методы их начисления

Денежные потоки и методы их оценки

Тема 2. Методологические основы принятия финансовых решений

Оглавление

2.1. Денежные потоки и методы их оценки 2.1.1. Процентные ставки и методы их начисления 2.1.2. Денежные потоки 2.1.3. Оценка аннуитетов. 2.2. Методы оценки финансовых активов 2.2.1. Внутренняя стоимость финансового актива 2.2.2. Подходы к оценке внутренней стоимости финансового актива 2.2.3. Внутренняя стоимость акций и облигаций 2.3. Риск в финансовом менеджменте 2.3.1. Понятие риска 2.3.2. Виды рисков 2.3.3. Оценка и анализ риска 2.3.4. Управление риском 2.4. Принятие решений в условиях риска и неопределенности 2.4.1. Элементы принятия финансовых решений 2.4.2. Принятие решений в условиях определенности и риска 2.4.3. Принятие решений в условиях неопределенности 2.5. Риск и доходность финансовых активов 2.5.1. Понятие и измерение доходности финансового актива 2.5.2. Доходность облигаций 2.5.3. Доходность акции 2.5.4. Оценка риска финансовых активов 2.6. Риск и доходность портфельных инвестиций 2.6.1. Понятие, цели и типы портфельного инвестирования 2.6.2. Оценки риска и доходности инвестиционного портфеля 2.6.3. Формирование инвестиционного портфеля Выводы. Вопросы для самопроверки Библиография

Версия для печати Хрестоматия Практикумы Презентации

Одной из важнейших базовых концепций финансового менеджмента является концепция временной ценности денег. Финансовые вычисления, базирующиеся на понятии временной ценности денег, используются в различных разделах финансового менеджмента при принятии решений о покупке или продаже финансовых активов, о вложениях в те или иные инвестиционные проекты и пр.

Логика финансовых вычислений с учетом временной ценности денег состоит в следующем. Предположим, что в настоящий момент бизнесмен располагает определенной суммой Р V (present value). Он может вложить эту сумму в бизнес или ценные бумаги, может дать в долг, вложить в банк. По прошествии определенного времени он рассчитывает получить большую сумму FV (future value). Результат его действий (эффект) может быть оценен при помощи получаемого абсолютного прироста стоимости:

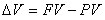
(2.1.1)

где РV – настоящая стоимость;

FV – будущая стоимость;

Δ V – прирост стоимости (прибыль).

Эффективность действий определяется путем расчета относительного показателя. Очевидно, что прирост стоимости можно соотнести с настоящей и с будущей суммой:

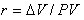или .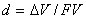

Если эти показатели рассчитываются в процентах, то первый (r) называется процентной ставкой, второй (d) – учетной ставкой. В финансовых вычислениях обычно пользуются процентной ставкой (представленной в долях от единицы). Таким образом в любой простейшей финансовой сделке всегда присутствуют три величины: имеющаяся (настоящая) сумма денег – РV, возвращаемая (будущая) сумма – FV, и процентная ставка – r, две из которых заданы, а одна является искомой.

Процесс, в котором известны исходная сумма и процентная ставка, и требуется определить будущую стоимость, в финансовых вычислениях называется процессом наращения (компаундирования). В этом случае рассматривается движение денежного потока от настоящего к будущему:

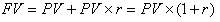
(2.1.2)

где r – ставка наращения.

Экономический смысл финансовой операции наращения состоит в определении величины той суммы, которую получит (хочет получить) инвестор по окончании этой операции. Для инвестора сумма PV в настоящий момент и FV через определенный интервал времени являются эквивалентными.

Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и процентная ставка, называется процессом дисконтирования. В этом случае речь идет о движении денежного потока от будущего к настоящему:

PV = FV / (1+ r),

(2.1.3)

где r – ставка дисконтирования.

Если в качестве ставки дисконтирования используется процентная ставка (r), соответствующий процесс называется математическим дисконтированием, если используется учетная ставка (d) имеет место банковское дисконтирование.

Экономический смысл дисконтирования заключается в определении суммы денег в настоящий момент, которую можно считать эквивалентной той сумме, которая будет у бизнесмена через определенный интервал времени. Ставка дисконтирования показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор на инвестируемый им капитал.

Необходимость учета временной ценности денег наиболее ярко проявляется в ссудо-заемных операциях. Предоставляя свои денежные средства в долг, их владелец получает определенный доход в виде процентов. Процентная ставка обычно устанавливается в виде годовой ставки, хотя возможно начисление процентов (выплата дохода) ежемесячно или один раз в полгода.

Существуют две схемы дискретного начисления процентов: схема простых и схема сложных процентов.

Схема простых процентов предполагает, что в каждом периоде проценты начисляются на исходную сумму, т.е. база, с которой начисляются проценты, остается неизменной. В этом случае ежегодно исходный инвестируемый капитал Р V возрастает на r процентов (r – требуемая доходность), т.е. на величину PV × r (r – в долях от единицы). Таким образом, размер инвестированного капитала FV через n лет будет равен:

,

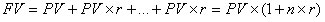(2.1.4)

Схему простых процентов используют в практике банковских расчетов при начислении процентов по краткосрочным ссудам со сроком погашения до одного года. В этом случае в качестве показателя n берут отношение длины периода, за который начисляются проценты, в днях к количеству дней в году.

Другой весьма распространенной операцией краткосрочного характера с использованием формулы простых процентов является операция по учету векселей банком. В этом случае используется учетная ставка:

,

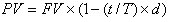(2.1.5)

где d — годовая учетная ставка в долях единицы;

t — продолжительность финансовой операции в днях;

Т — количество дней в году.

Схема сложных процентов предполагает, что в каждом последующем периоде проценты начисляются не на исходную сумму, а на общую сумму, включающую и ранее начисленные, невостребованные инвестором проценты. В этом случае происходит капитализация (реинвестирование) процентов по мере их начисления, т.е. база, с которой начисляются проценты, все время возрастает.

Поэтому, сумма денег к концу n -го года будет равна:

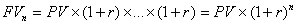
(2.1.6)

Множитель (1+r)ⁿ показывает, чему будет равна одна денежная единица (один рубль, один доллар, один евро и т.п.) через n периодов при заданной процентной ставке r.

Можно показать, что в случае ежегодного начисления процентов для лица, предоставляющего кредит:

· более выгодна схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);

· более выгодна схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно, в этой ситуации капитал, генерирующий доходы, постоянно возрастает);

· обе схемы дают одинаковые результаты при продолжительности периода один год и однократном начислении процентов.

При проведении расчетов необходимо помнить, что периодом выступает срок, за который происходит однократное начисление процентов. Так, если за базисный период начисления процентов взят квартал, то в расчетах должна использоваться квартальная ставка.

В банковской практике типичной является ситуация, когда в договоре указывается годовая процентная ставка с частотой начисления процентов меньше года. В этом случае расчет ведется по формуле сложных процентов, где в качестве периода берется не год, а интервал начисления процентов:

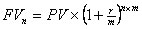
(2.1.7)

где r — объявленная годовая ставка; т — количество начислений в году; n — количество лет.

Для сравнения вложений, по которым предусматриваются различные процентные ставки и различные интервалы начисления процентов, рассчитывается эффективная годовая процентная ставка, показывающая, на сколько процентов фактически увеличится сумма вложений за год:

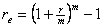
(2.1.8)

где r – объявленная (номинальная) годовая ставка процента;

r_e– эффективная годовая процентная ставка.

При начислении процентов раз в год номинальная и эффективная ставки совпадают, при большем количестве начислений эффективная ставка больше номинальной.

Дата добавления: 2014-01-03