Оценка аннуитетов

Частный случай денежного потока, в котором денежные поступления в каждом периоде одинаковы по величине, носит название аннуитета. Если число равных временных интервалов ограничено, аннуитет называется срочным. В этом случае

С1=С2=...=С n =А.

Для оценки будущей и настоящей стоимости аннуитета можно пользоваться вышеприведенными формулами, вместе с тем благодаря специфике аннуитетов, заключающейся в равенстве денежных поступлений эти формулы могут быть существенно упрощены. Если в формулах настоящей и будущей стоимости денежного потока заменить C_t на А и вынести этот множитель за знак суммы, то под знаком суммы останется сумма первых n членов геометрической прогрессии. Применив известную из алгебры формулу, можно получить следующие упрощенные формулы для оценки аннуитета:

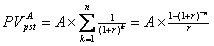
	(2.1.14)
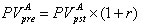
	(2.1.15)
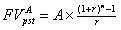
	(2.1.16)
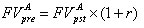
	(2.1.17)

Предполагается, что денежные суммы лишь начисляются, а изъять их можно по окончании срока действия аннуитета.

Аннуитет называется бессрочным, если денежные поступления продолжаются достаточно длительное время (в западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет).

В этом случае задача оценки будущей стоимости аннуитета смысла не имеет. Настоящая стоимость определяется с использованием формулы для расчета суммы членов бесконечной геометрической прогрессии:

PV = A / r

(2.1.18)

Эта формула служит для оценки целесообразности приобретения бессрочного аннуитета. В данном случае известен размер годовых поступлений; в качестве ставки дисконтирования r обычно принимают гарантированную процентную ставку (например, процент, предлагаемый государственным банком).

Логика, заложенная в схему аннуитетных платежей, широко используется при оценке долговых и долевых ценных бумаг, в анализе инвестиционных проектов, а также в анализе аренды.

Дата добавления: 2014-01-03