Оценки риска и доходности инвестиционного портфеля

Главная проблема в формировании портфеля инвестиций состоит в обеспечении оптимального соотношения между риском и доходностью. Правило: чем более высокий доход приносит ценная бумага, тем больший потенциальный риск она имеет. Решается эта проблема, прежде всего на основе диверсификации портфеля (т.е. распределения средств между различными активами) и тщательного подбора фондовых инструментов.

Очевидно, что доходность портфеля (dp) представляет собой линейную функцию показателей доходности входящих в него активов и может быть рассчитана по формуле средней арифметической взвешенной (в данном случае речь может идти как об ожидаемой, так и о фактической доходности):

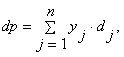
(2.6.1)

где dj — доходность j -го актива;

yj — доля j -го актива в портфеле;

n — число видов активов в портфеле.

Следует помнить, что формирование портфеля из наиболее доходных активов в общем случае приводит к увеличению его риска.

Мерой риска портфеля, как и отдельного актива, служит вариабельность его доходности. Взаимосвязь между риском портфеля и риском входящих в него активов не описывается формулой средней арифметической. Как известно из курса статистики, в многомерном случае необходимо учитывать взаимосвязь значений доходности активов портфеля с помощью показателя ковариации и коэффициента корреляции.

В частности, если в качестве меры риска актива выступает среднее квадратическое отклонение, то его значение для портфеля, содержащего k видов активов, может быть найдено по формуле:

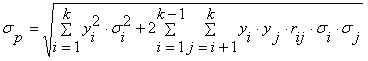
(2.6.2)

где σ_p – мера риска портфеля;

y_i— доля i -го актива в портфеле;

σ_i — вариация доходности i -го актива;

r_ij — коэффициент корреляции между ожидаемыми доходностями i -го и j -го активов.

Для портфеля из двух активов эта формула существенно упрощается и имеет вид:

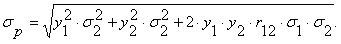
(2.6.3)

Из приведенных формул следуют выводы:

1) риск, ассоциируемый с каким-то конкретным активом, не может рассматриваться изолированно от всего портфеля, т.е. любая новая инвестиция должна анализироваться с позиции ее влияния на изменение доходности и риска инвестиционного портфеля в целом;

2) если доходность портфеля равна средней доходности входящих в него активов, то риск портфеля может быть как больше, так и меньше среднего значения; при определенном сочетании активов можно добиться значительного снижения риска портфеля;

3) риск портфеля зависит не от значений доходности, а от их вариации; кроме этого риск портфеля зависит от количества активов в портфеле, структуры портфеля, рисковости и динамики доходности его составляющих.

4) разнонаправленность тенденций финансовых активов, приводящих к отрицательному значению коэффициента корреляции, способствует снижению риска портфеля (если портфель состоит из двух активов, связанных обратной функциональной зависимостью, то его риск равен нулю).

5) добавление в портфель безрискового актива уменьшает доходность портфеля, при этом риск портфеля уменьшается прямо пропорционально доле этого актива;

6) объединение рисковых активов в портфель может приводить к снижению риска по сравнению с обладанием каждым из этих активов в отдельности, однако результат зависит не только от рисковости объединяемых активов, но и от характера взаимосвязи между их доходностями. В общем случае риск комбинации активов меньше среднего риска объединяемых активов;

7) при объединении в портфель независимых активов (в этом случае значения парных коэффициентов корреляции равны нулю) риск портфеля находится как среднее взвешенное рисков отдельных активов, формирующих портфель:

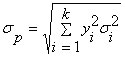
(2.6.4)

8) если имеются на выбор два актива с одинаковыми характеристиками, однако доходность одного из них меняется однонаправленно, а доходность второго — разнонаправленно с доходностью портфеля, то с позиции минимизации риска для включения в портфель следует предпочесть второй актив.

При формировании портфеля теоретически могут ставиться три основные целевые задачи: 1) достижение максимально возможной доходности; 2) получение минимально возможного риска; 3) получение некоторого приемлемого соотношения «доходность/риск».

Первая задача решается путем формирования портфеля из одного наиболее доходного актива; вторая – из одного наименее рискового (безрискового) актива. В действительности смысл формирования портфеля состоит в поиске комбинации активов, обеспечивающей рост (неснижение) доходности при снижении (невозрастании) риска. Эта задача не имеет однозначного решения.

Дата добавления: 2014-01-03