
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство
|
|
|
|
Лекция
Свойства:
9) Пусть ϕ(x) строго выпуклая функция на выпуклом множестве и существует глобальный минимум, тогда он единственный.
10) Глобальный максимум выпуклой функции ϕ(x) на выпуклом множестве совпадает хотя бы с одной экстремальной точкой этого множества.
□ От противного:
Пусть есть  =
=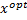
Пусть 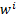 ≠
≠  - экстремальная точка, где i=
- экстремальная точка, где i=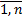 . Докажем, что это не так:
. Докажем, что это не так:
По теореме о представлении 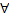 точка
точка  =
=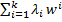 ;
; 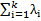 =1, 𝝀≥0.
=1, 𝝀≥0.
Кроме того, для тех же 𝝀 можно применить неравенство Йенсена:
ϕ (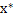 )≤
)≤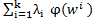
Возьмем max ϕ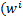 )=
)=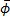 . Подставим в правую часть:
. Подставим в правую часть:
ϕ (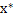 )≤
)≤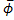 =
= 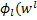 ), следовательно противоречие и
), следовательно противоречие и  =
=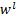 . □
. □
11) Пусть имеется дифференцируемая выпуклая функция ϕ во всех точках выпуклого открытого множества X, тогда необходимым и достаточным условием выпуклости этой функции является следующее неравенство: ∀ 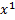 ,
,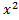 ϵX
ϵX
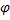 (
(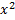 )≥ ϕ(
)≥ ϕ(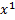 )+
)+ 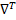 ϕ (
ϕ (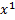 )(
)(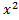 -
-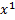 ), где
), где 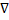 ϕ (
ϕ (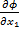 ,…,
,…, 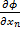
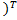
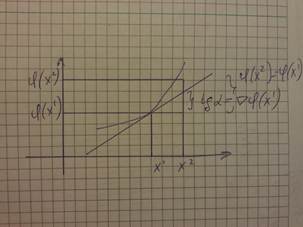
12) Точка 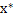 является точкой глобального минимума для выпуклой, непрерывной дифференцируемой функции на выпуклом открытом множестве X тогда и только тогда, когда выполняется следующее неравенство:
является точкой глобального минимума для выпуклой, непрерывной дифференцируемой функции на выпуклом открытом множестве X тогда и только тогда, когда выполняется следующее неравенство:
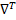 ϕ (
ϕ ( )(
)(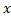 -
- )≥0, ∀ xϵ X (1)
)≥0, ∀ xϵ X (1)
Следствие:
Если x- открытое множество и  ϵX, то в этой точке
ϵX, то в этой точке 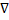 ϕ(
ϕ( )=0
)=0
Доказательство:
□ В качестве переменной возьмем следующую точку xϵ X, x= -α
-α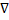 ϕ(
ϕ( ), α
), α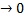
Отсюда видно, что если подставить в (1), то получим следующее: ||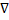 ϕ(
ϕ( )||≥0, следовательно
)||≥0, следовательно 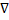 ϕ(
ϕ(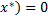 □
□
Опр: Точки, для которых градиент какой-либо точки равен 0 называются стационарными точками.
Стационарная точка- это необходимое условие для открытого множества существования экстремума.
И оно становится и достаточным, если функция выпуклая(вогнутая): в первом случае минимум, во втором максимум.
Данное условие позволяет выбирать направления, допустимые во внутренней области. Например 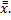 Очевидно, что для нее
Очевидно, что для нее 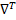 ϕ(
ϕ(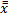 )(
)(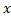 -
-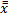 )
)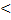 0,
0, 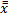 ≠opt
≠opt
13) Свойство матрицы Гессе для непрерывных и дважды дифференцируемых выпуклых функций
Теорема:
Пусть имеется непрерывная дважды дифференцируемая функция ϕ(x), определенная на выпуклом открытом множестве X. Тогда и только тогда функция является выпуклой, когда матрица Гессе на всем множестве X не отрицательно определена. Т.е. H(x)≥0, ∀xϵX (не положительно определена, когда функция вогнута).
H(x)=((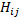 ))
))
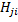 =
=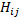 =
=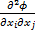
Доказательство:
□ (Для выпуклой функции)
Пусть 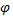 - непрерывная, выпуклая, дважды дифференцируемая функция. Тогда ϕ(x) диф. В какой-либо точке
- непрерывная, выпуклая, дважды дифференцируемая функция. Тогда ϕ(x) диф. В какой-либо точке 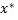 ϵ X и имеем:
ϵ X и имеем:
1) ϕ(x)= ϕ( )+
)+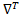 ϕ (
ϕ ( )(
)(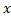 -
- ) +
) +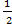
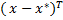 H (
H ( )(
)(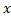 -
- ) +O(
) +O(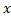 -
- ) ||
) ||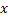 -
- ||2
||2
2) (из свойства 11) ϕ(x)≥ ϕ( ) +
) +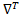 ϕ (
ϕ ( )(
)(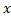 -
- )
)
Подставим в 11 свойство и устремим x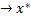 , получим:
, получим:
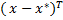 H (
H ( )(
)(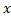 -
- )≥0
)≥0
H ( )≥0, ∀
)≥0, ∀ 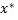 ϵ Х □
ϵ Х □
Обратная теорема:
Пусть x- малое открытое множество на котором матрица Гессе неотрицательно определена, тогда функция ϕ на этом множестве выпукла.
Доказательство:
Возьмем две произвольные точки 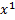 ,
,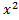 ϵX. Возьмем точку
ϵX. Возьмем точку 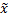 = λ
= λ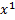 +(1-𝝀)
+(1-𝝀)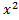 ,
, 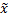 ϵ [
ϵ [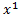 ,
,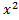 ], 𝝀ϵ[0,1]
], 𝝀ϵ[0,1]
Вспомним теорему Тейлора: если у нас есть некий отрезок [ 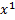 ,
,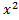 ], то
], то
ϕ (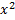 )= ϕ (
)= ϕ (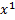 )+
)+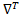 ϕ (
ϕ (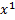 )(
)(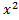 -
-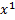 )+
)+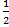
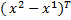 H (
H (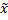 )(
)(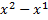 )
)
Получаем нер-во из свойства 11: ϕ (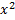 )≥ϕ (
)≥ϕ (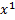 )+
)+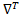 ϕ (
ϕ (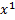 )(
)(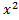 -
-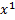 ), следовательно ϕ-выпуклая. □
), следовательно ϕ-выпуклая. □
Пример:
ϕ (x)=2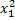 + 3
+ 3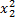 , пусть xϵ
, пусть xϵ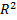
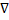 ϕ=
ϕ= 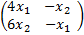 H
H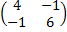 -?
-?
Det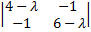 =0
=0
(𝝀-4)(𝝀-6) -1=0
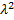 -10𝝀+23=0
-10𝝀+23=0
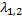 =
=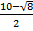 ≥0,
≥0,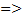 выпукл.
выпукл.
14) Достаточное условие для стационарной точки ϕ(x), X-открытое  ϵX-стационарная точка
ϵX-стационарная точка
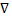 ϕ(
ϕ( )=0
)=0
Достаточным условие локального минимума(максимума) является следующее условие:
H( )
)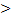 0 (H(
0 (H( )
)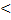 0)
0)
X=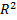 - открытое
- открытое
1)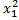 +
+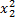 -выпуклое
-выпуклое
2)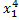 +
+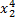 - выпуклое
- выпуклое
3)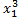 +
+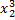 - не выпуклое и не вогнутое
- не выпуклое и не вогнутое
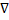 ϕ(
ϕ( )=0
)=0
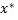 =
=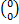
1)H(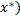 =
=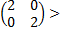 0
0
2,3)H=0
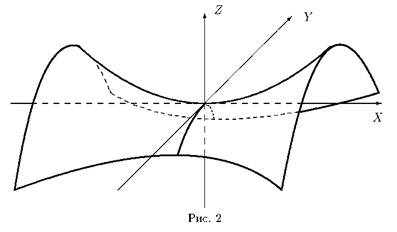
Если матрица Гессе на открытом множестве имеет переменный знак, то там может быть седло.
Опр: Пусть у нас есть 2 группы переменных 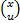
Пусть x ϵ X, u ϵ U, тогда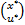 называется седлом функции ϕ(x), если выполняется следующее условие:
называется седлом функции ϕ(x), если выполняется следующее условие:
(3 определения)
1) ϕ(x,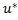 )≤ϕ(
)≤ϕ(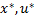 )≤ϕ(
)≤ϕ(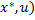
2) 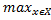 ϕ(x,
ϕ(x,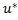 )=
)=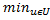 ϕ(
ϕ(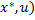
3) 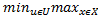 ϕ(x,u)=
ϕ(x,u)=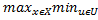 ϕ(x,u)
ϕ(x,u)
Седло может быть как на открытом множестве так и на компактах.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 512; Нарушение авторских прав?; Мы поможем в написании вашей работы!