Дисперсия случайной величины

Математическое ожидание случайной величины.

Математическим ожиданием дискретной случайной величины X называют сумму произведений всех её возможных значений на их ве­роятности: для дискретной случайной величины X, принимающей значения x ₁, x ₂,..., x_n с вероятностями соответственно p ₁, p ₂,..., p_n соответственно, имеем:

В частном случае, когда все значения x _i равновероятны, т.е. , математическое ожидание равно

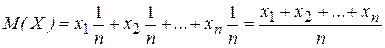- среднему арифметическому всех возможных значений случайной величины. Поэтому математическое ожидание называют также средним значением случайной величины.

Математическое ожидание случайной величины – это число, которое показывает, какое значение случайной величины можно ожидать в среднем при проведении серии опытов.

Пусть значения непрерывной случайной X принадлежат отрезку [ а, b ]. Математическим ожиданием непрерывной случайной величины X называется величина:

.

где f(x) - плотность распределения вероятностей случайной величины Х.

Дисперсией (рассеянием) D(X) случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X)=M((X-M(X))²).

Дисперсию удобно вычислять по формуле: D(X)=M(X²)-(M(X))².

Дисперсией (рассеянием) D(X) дискретной случайной величиной X является величина:

Дисперсией D(X) непрерывной случайной величины X является величина:

где f(x) - плотность распределения вероятностей случайной величины Х.

Если возможные значения непрерывной случайной X принадлежат всей числовой оси, то пределы интегрирования берутся от -R до R.

Средним квадратическим отклонением называют корень квадратный из дисперсии:

Модой Мо непрерывной случайной величины Х называется такое ее значение, которому соответствует максимальное значение ее плотности распределения вероятностей.

Медианой Ме непрерывной случайной величины Х называется такое ее значение, которое определяется равенством: Р(Х<Ме(Х))=Р(Х>Ме(Х)).

Пример. По заданному закону распределения случайной величины Х найти ее математическое ожидание, дисперсию и среднее квадратическое отклонение.

Х
р	0.1	0.4	0.2	0.2	0.1

Решение.

М(Х) = 4*0.1 + 7*0.4 + 8*0.2 + 10*0.2 + 12*0.1 = 8

D(X) = (4 - 8)²*0.1+(7 - 8)²*0.4+(8 - 8)²*0.2+(10 - 8)²*0.2+(12 - 8)²*0.2 = 4.4

s_x = 2.098

2.3. Статистическая совокупность

Для того, чтобы получить наиболее полную информацию об изучаемом явлении, необходимо анализировать результаты не отдельных наблюдений, а множества однородных наблюдений. Результаты отдельных наблюдений могут оказаться случайными, неполно выражать сущность изучаемого явления. Очевидно, что наблюдаемые объекты обладают множеством признаков; однако, поставив своей задачей изучение лишь одного признака, мы тем самым полагаем, что в отношении остальных объекты равноправны, то есть множество объектов однородно.

Некоторое множество относительно однородных объектов, объединяемых по тому или иному признаку для совместного изучения, называется статистической совокупностью. Отдельные объекты статистической совокупности называются членами совокупности.

Дата добавления: 2014-01-03