Метрика сигналов

Линейное пространство сигналов L является метрическим, если каждой паре сигналов s(t) Î L и v(t) Î L однозначно сопоставляется неотрицательное число r(s,v) – метрика (metric) или расстояние между векторами. Пример метрики для двух векторов в двумерном пространстве приведен на рис. 2.2.

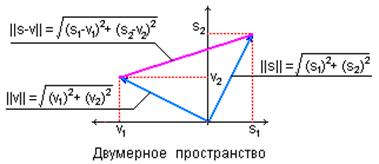
Рис. 2.2. Норма и метрика сигналов

Для метрик сигналов в метрическом пространстве любой размерности должны выполняться аксиомы:

1. r(s,v) = r(v,s) – рефлексивность метрики.

2. r(s,s) = 0 для любых s(t) Î L.

3. r(s,v) £ r(s,a) + r(a,v) для любых a Î L.

Метрика определяется нормой разности двух сигналов (см. рис. 2.2):

r(s,v) = || s(t) – v(t) ||. (2.3)

В свою очередь норму можно отождествлять с расстоянием от выбранного элемента пространства до нулевого: ||s(t)|| = r(s(t),Æ).

По метрике сигналов можно судить, например, о том, насколько точно один сигнал может быть аппроксимирован другим сигналом, или насколько изменяется выходной сигнал относительно входного при прохождении через какое-либо устройство.

Пример. Сигнал на интервале (0,Т) представляет собой половину периода синусоиды амплитудой A: s(t) = A×sin(pt/T), 0 £ t £ T. Требуется аппроксимировать сигнал прямоугольным импульсом п(t) (см. рис. 2.3).

Если принять амплитуду импульса п(t) равной В, то квадрат расстояния между сигналами: r²(s,п) =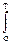(A sin(pt/T)-В)² dt = A²T/2 - 4ABT/p + B²T.

Для решения задачи требуется найти минимум выражения r²(s,п). Дифференцируем полученное выражение по В, приравниваем нулю и, решая относительно В, находим значение экстремума: В = 2A/p» 0.64А. Это искомое значение минимума функции r²(s,п) (вторая производная функции по В положительна). При этом минимальное значение метрики: r_min» 0.31A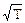. Вычислим нормы сигналов при А = 1:

Е_s = А²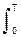sin² (pt/T) dt = A² T/2 = 10. Норма: ||s(t)|| =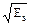= 0.707 A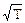» 3.16.

Е_п = B²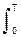dt = B² T» 8.1. Норма: ||п(t)|| = 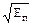= B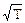» 2.85.

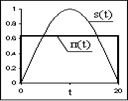
Рис. 2.3

Метрика (2.3) не единственно возможная. Пространство сигналов может иметь несколько метрик. Так, для дискретных сигналов, заданных на интервале Т, могут задаваться метрики по модулю разности и по максимуму модуля разности:

r₁(s,v) =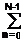|s_n - v_n|, r₁(s,v) = max_n |s_n - v_n|.

Метрика в пространстве N-разрядных двоичных сигналов х и у для любой парой таких сигналов вполне будет определяться числом несовпадающих символов, которое называют расстоянием по Хеммингу для двоичных слов:

r(x,y) =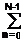[s_n ⊕ v_n],

где знак Å означает сложение по модулю 2 (1+0 = 0+1 = 1, 0+0 = 1+1 = 0 без переноса в старший разряд).

Дата добавления: 2014-01-03