Метод узловых потенциалов

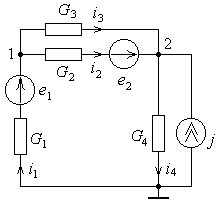Рис. 8.1.

Этот метод используется для расчета напряжений и токов эл. цепей. Идея метода состоит в том, что напряжения и токи ветвей эл. цепи выражаются через потенциалы узлов. При этом уравнения контуров выполняются автоматически (см. пример п. 3), а количество неизвестных и уравнений существенно сокращается.

Метод узловых потенциалов удобен еще и тем, что потенциалы узлов можно измерить вольтметром или наблюдать с помощью осциллографа, сравнивая расчеты с экспериментами.

Рассмотрим эл. цепь (рис. 8.1). Поставим задачу найти напряжения и токи всех ветвей цепи.

Вначале устраним неоднозначность узловых потенциалов. Если ко всем ним прибавить одно и то же число, то разности потенциалов, а значит, напряжения и токи цепи, не изменятся. Поэтому можно заранее считать, что мы прибавили к потенциалам такое число, что потенциал выбранного нами узла оказался равным нулю. Такой узел называется базовым и обозначается знаком 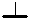. После выбора базового узла потенциалы определяются однозначно.

Запишем уравнения первого закона Кирхгофа для всех узлов, кроме одного (любого). Пусть в нашем случае это будут узлы 1, 2:

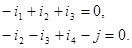(8.1)

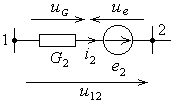Рис. 8.2.

Выразим токи ветвей через узловые потенциалы. Для ветви, состоящей из e ₂ и G ₂ (рис. 8.2), получим:

– по 2‑му закону Кирхгофа ,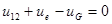

– по определению напряжения между двумя точками ,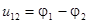

– по уравнению источника напряжения ,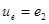

– согласно уравнению резистора .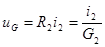

Окончательно получаем .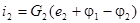

Аналогично для остальных ветвей с учетом того, что потенциал базового узла равен нулю, получим: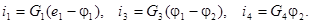

Подставим выражения для токов в уравнения (8.1), получим:

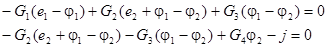
Сгруппировав слагаемые, преобразуем полученную систему уравнений к виду

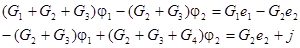
Запишем последнюю систему уравнений в матричной форме:

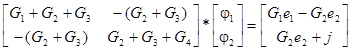(8.2)

Решив эту систему уравнений, получим значения узловых потенциалов. Затем можно будет найти токи ветвей по записанным выше формулам и напряжения ветвей как разности потенциалов узлов.

Систему уравнений (8.2) можно составить непосредственно по схеме эл. цепи с помощью следующих правил:

1. На диагонали матрицы в k-й строке k-м столбце записывается сумма проводимостей ветвей, подключенных к k-му узлу.

2. В k-й строке m-м столбце записывается взятая со знаком "минус" сумма проводимостей ветвей, соединяющих узел № k и узел № m.

3. В k-й строке правой части системы уравнений записывается сумма токов короткого замыкания ветвей, подключенных к узлу № k. При этом ток входит в сумму с дополнительным знаком "минус", если стрелка соответствующего источника направлена от узла № k.

При составлении системы уравнений учитывается, что проводимость ветви, содержащей источник тока, равна нулю.

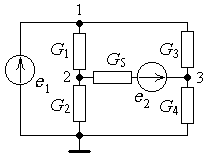Рис. 8.3.

Особый случай представляют цепи, в которых есть ветви, состоящие только из источников напряжения (рис. 8.3.). Проводимость таких ветвей бесконечна, поэтому ее нельзя записать в уравнения. Систему уравнений для расчета узловых потенциалов таких цепей можно составить с помощью специальных приемов, простейший из которых - введение в ветви с нулевым сопротивлением некоторых малых резисторов.

Дата добавления: 2014-01-03