
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Биномиальное распределение
Пусть проводится эксперимент, в результате которого нас интересует, произошло событие А или не произошло. Случай, в котором событие А произошло, назовем успехом, вероятность этого события Р(А) =р Если же событие А не произошло, то его вероятность P(A’) =1-p = q
Дискретная случайная величина X распределена по биномиальному закону, если ее возможные значения 0,1,2, ...т,..л, а вероятность появления таких значений определяется соотношением:
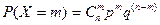 (9)
(9)
Закон называется биноминальным, т.к. в правой части формулы разложение бинома (p+q)n. Величина
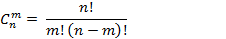
число сочетаний из n элементов по m.
В общем виде:
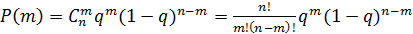 (10)
(10)
Где 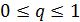
Например, производится n. последовательных независимых опытов, в каждом из которых вероятность осуществления события А постоянна и равна q Тогда вероятность того, что событие А произойдет точно т раз (если не учитывается порядок осуществления событий) определяется соотношением (10).
Применительно к выборочному контролю качества продукции по альтернативному признаку биномиальному распределению подчиняется количество несоответствующих единиц продукции (m) в повторных выборках объемом п, взятых из контролируемой партии продукции с уровнем несоответствия, равным q.
Рассмотрим такой случай. В партии содержится N изделий (M – бракованных, N-M - годных). Вероятность извлечения годного изделия 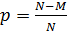 бракованного
бракованного 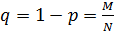 . Из партии берут изделие, проверяют его качество, после чего возвращают в партию и перемешивают. Затем берут наугад второе изделие, производят те же самые операции и т.д. Вероятность извлечения (n-m) годных изделий из проконтролированных определятся по формуле
. Из партии берут изделие, проверяют его качество, после чего возвращают в партию и перемешивают. Затем берут наугад второе изделие, производят те же самые операции и т.д. Вероятность извлечения (n-m) годных изделий из проконтролированных определятся по формуле
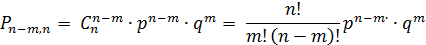
Параметры биномиального распределения
математическое ожидание равно M(x)=np,………………….(11)
дисперсия 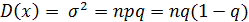
Для краткой записи биномиального распределения используют запись Bi(Mx, σ).
Для упрощения расчетов по формуле (10) удобно использовать следующие рекуррентные соотношения:
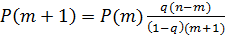 (12)
(12)
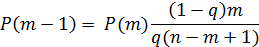
|
Дата добавления: 2014-01-03; Просмотров: 557; Нарушение авторских прав?; Мы поможем в написании вашей работы!