Гипергеометрическое распределение

Законы распределения дискретных величин

Законы распределения случайных величин

При контроле качества используются законы распределения дискретных и непрерывных случайных величин.

Наиболее распространены три типа распределения дискретных случайных величин гипергеометрическое распределение, биноминальное распределение и распределение Пуассона.

Дискретная случайная величина X с возможными значениями 0,1,2,...m,..М имеет гипергеометрическое распределение с параметрами n,N и. M, если вероятность того, что она примет значение, равное т, определяется соотношением:

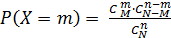) (5)

Где ,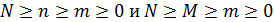

N и n –объем партии и выборки

M и m – количество дефектных единиц продукции в партии и выборке.

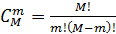- число сочетаний из М по m.

Гипергеометрическое распределение типично для выборочного контроля качества продукции по альтернативному признаку. В этом случае генеральной совокупностью является контролируемая партия продукции объемом N, в которой М единиц продукции несоответствующие. Если из этой партии продукции берется безвозвратная выборка объемом п, то количество несоответствующих изделий в выборке является дискретной случайной величиной, подчиняющейся гипергеометрическому закону распределения. Таким образом, вероятность того, что в выборке объемом п будет обнаружено ровно m несоответствующих изделий, определяется соотношением (5).

На практике для упрощения расчетов можно использовать рекуррентные соотношения

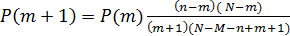(6)

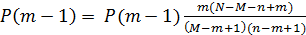
При использовании рекуррентных соотношений для уменьшения погрешности округления сначала вычисляют 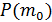, а затем применяют как восходящую рекурсию для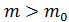так и убывающую - для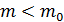

Приведем без доказательства выражение для параметров гипергеометрического распределения:

математическое ожидание 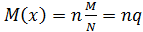; (7)

дисперсия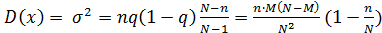

Если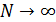, в то время как п и 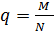остаются фиксированными, то гипергеометрическое распределение стремится к биномиальному распределению. Это объясняется тем, что бесповторная выборка мало отличается от повторной выборки, если соотношение мало. Аппроксимация биномиальным распределением применима при условии, 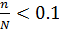, и вместо выражения 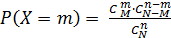можно использовать соотношение биномиального распределения.

Дата добавления: 2014-01-03