
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Конечные приближения идеальных фильтров
|
|
|
|
Оператор идеального частотного НЦФ, как это следует из выражения (7.2.2), представляет собой бесконечную затухающую числовую последовательность, реализующую заданную передаточную функцию:
H(w) =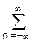 h(n) cos nw. (7.3.1)
h(n) cos nw. (7.3.1)
Ограничение окна операторов фильтров. На практике бесконечный ряд (7.3.1) всегда приходится ограничивать определенным числом членов его конечного приближения
H'(w) =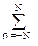 h(n) cos nw,
h(n) cos nw,
при этом передаточная функция осложняется явлением Гиббса, и появляется переходная зона между полосами пропускания и подавления сигнала (рис. 7.3.1, пунктирная кривая при N=100). Явление Гиббса формирует первые выбросы передаточной функции на расстоянии p/(2(N+1)) от скачков (разрывов первого рода). Если ширину переходной зоны Dp в первом приближении принять по расстоянию между первыми выбросами по обе стороны от скачка функции H(w), то ее значение будет ориентировочно равно p/(N+1) = Dp.
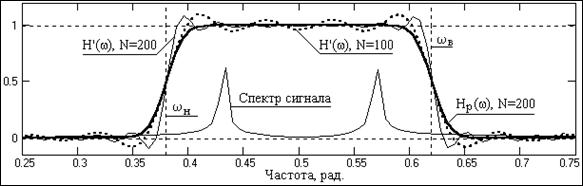
Рис. 7.3.1. Передаточные функции полосового фильтра.
Применение весовых функций. Если уровень пульсаций передаточной функции, определяемый явлением Гиббса, не удовлетворяет поставленным задачам фильтрации данных, рекомендуется использование сглаживающих весовых функций. С учетом того, что при применении весовых функций происходит расширение переходных зон примерно в два раза, значение ширины переходной зоны будет равным Dp = 2p/N. Отсюда можно определить минимальное число членов усеченного ряда по заданному размеру переходной зоны:
N = 2p/Dp. (7.3.2)
Для примера на рис. 7.3.1 значение N принято равным 200, при этом крутизна переходной зоны увеличилась (тонкая кривая H'(w), N=200), создавая запас на последующее сглаживание весовой функцией.
Выбор весовых функций целесообразно осуществлять по допустимой величине осцилляций усиления сигнала в полосе подавления, т.е. по относительному значению амплитуды первого выброса на передаточных характеристиках весовых функций. Для выбранной весовой функции (с учетом числа ее членов по (7.3.2)) производится расчет весовых коэффициентов pn, после чего устанавливаются окончательные значения оператора фильтра:
hn = pn h(n). (7.3.3)
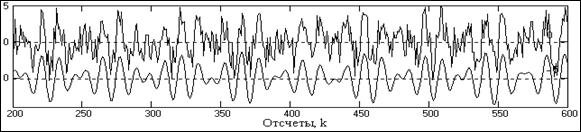 Рис. 7.3.2. Полосовая фильтрация (вверху – входной сигнал, внизу – выходной).
Рис. 7.3.2. Полосовая фильтрация (вверху – входной сигнал, внизу – выходной).
|
Подстановкой коэффициентов (7.3.3) в (7.3.1) рекомендуется произвести построение полученной передаточной характеристики фильтра и непосредственно по ней оценить пригодность фильтра для поставленных задач. Это наглядно видно на рис. 7.3.1, где для нашего примера была применена весовая функция Гаусса. Передаточная функция Hp(w) имеет практически такую же крутизну, как и функция H'(w) при N=100 и практически плоскую вершину в интервале спектра сигнала. Качество работы фильтра для сигнала, приведенного на рис. 7.2.1, можно видеть на рис. 7.3.2.
При необходимости более точной оценки полученной передаточной функции можно рекомендовать увеличение ее частотного разрешения в 2-4 раза перед выполнением преобразования Фурье, что можно выполнить путем увеличения размеров оператора hn дополнением нулями.
Основные весовые функции. Ниже в таблицах приведены формулы и основные спектральные характеристики наиболее распространенных весовых окон. Носители весовых функций, в принципе, являются неограниченными и при использовании в качестве весовых окон действуют только в пределах окна и обнуляются за его пределами. Для упрощения записи формулы приводятся в аналитической форме с временным окном 2t, симметричным относительно нуля (0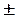 t). При переходе к дискретной форме окно 2t заменяется окном 2N+1, а значения t – дискретами t = nDt. Большинство весовых функций на границах окна (n =
t). При переходе к дискретной форме окно 2t заменяется окном 2N+1, а значения t – дискретами t = nDt. Большинство весовых функций на границах окна (n = 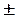 N) принимают нулевые или близкие к нулевым значения. Последнее исключается, если принять 2t = (2N+3)Dt, при этом близкие к нулю значения перемещаются за границы окна.
N) принимают нулевые или близкие к нулевым значения. Последнее исключается, если принять 2t = (2N+3)Dt, при этом близкие к нулю значения перемещаются за границы окна.
Основные весовые функции.
| Временное окно | Весовая функция | Фурье-образ |
| Естественное (П) | П(t) = 1, |t|£t; П(t) = 0, |t|>t | П(w) = 2t sinc[wt] |
| Бартлетта (D) | b(t) = 1-|t|/t | B(w) = t sinc2(wt/2). |
| Хеннинга, Ганна | p(t) = 0.5[1+cos(pt/t)] | 0.5П(w)+0.25П(w+p/t)+0.25П(w-p/t) |
| Хемминга | p(t) = 0.54+0.46 cos(pt/t) | 0.54П(w)+0.23П(w+p/t)+0.23П(w-p/t) |
| Карре (2-е окно) | p(t) = b(t) sinc(pt/t) | t·B(w)*П(w), П(w) = 1 при |w|<p/t |
| Лапласа-Гаусса | p(t) = exp[-b2(t/t)2/2] | [(t/b)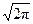 exp(-t2w2/(2b2))] ③ П(w) exp(-t2w2/(2b2))] ③ П(w)
|
| Кайзера-Бесселя | p(t) =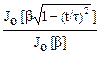 ,
Jo[x] = ,
Jo[x] =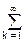 [(x/2)k/k!]2 [(x/2)k/k!]2
| Вычисляется преобразованием Фурье. Jo[x] - модифицированная функция Бесселя нулевого порядка |
Характеристики спектров весовых функций.
| Параметры | Ед. изм. | П- Окно | Барт- летт | Лан-цош | Хен- нинг | Хемминг | Кар- ре | Лаплас | Кайзер |
| Амплитуда: Главный пик 1-й выброс(-) 2-й выброс(+) Ширина Гл. пика Положения: 1-й нуль 1-й выброс 2-й нуль 2-й выброс | t %Гл.п. - “ - wt/2p wt/2p wt/2p wt/2p wt/2p | 0.217 0.128 0.60 0.50 0.72 1.00 1.22 | - 0.047 0.89 1.00 - - 1.44 | 1.18 0.048 0.020 0.87 0.82 1.00 1.29 1.50 | 0.027 0.0084 1.00 1.00 1.19 1.50 1.72 | 1.08 0.0062 0.0016 0.91 1.00 1.09 1.30 1.41 | 0.77 - - 1.12 - - - - | 0.83 0.0016 0.0014 1.12 1.74 1.91 2.10 2.34 | 0.82 .00045 .00028 1.15 1.52 1.59 1.74 1.88 |
Весовая функция Кайзера. Наибольшее распространение при расчетах частотных НЦФ получила весовая функция Кайзера:
p(n) =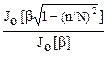 .
.
Это объясняется тем, что параметры функции Кайзера могут устанавливаться непосредственно по техническим требованиям к передаточным функциям проектируемых фильтров – допустимой ширине переходной зоны Dp и значению коэффициента шума фильтра d (максимальным значениям осцилляций передаточной функции в единицах коэффициента передачи в полосе пропускания).
Кайзером установлено, что для заданного значения d произведение количества членов оператора НЦФ на ширину переходной зоны является величиной постоянной. Оно получило название D-фактора:
D = N·Dp/p.
С другой стороны, установлены следующие эмпирические соотношения между D-фактором и параметром b функции Кайзера:
D = (А-7.95)/14.36 при А>21.
= 0.9222 при А<21.
b = 0.1102(A-8.7) при А>50.
= 0 при А<21.
= 0.5842(A-21)0.4 + 0.07886(A-21), 21<А<50.
где: А = -20 log d - затухание в децибелах.
Приведенные выражения позволяют по заданному значению коэффициента шума d определить параметр b функции Кайзера, а через D-фактор число членов фильтра:
N = pD/Dp.
При проектировании полосовых фильтров проверка передаточной функции полученного оператора НЦФ исходному заданию по значению коэффициента шума является обязательной. Это объясняется тем, что поскольку полоса пропускания полосового фильтра ограничена двумя скачками, на передаточной характеристике возникают два центра осцилляций, при этом наложение осцилляций может как уменьшить, так и увеличить амплитуду суммарных осцилляций. Если за счет наложения произойдет увеличение амплитуды осцилляций, то расчет НЦФ следует повторить с уменьшением исходного значения d.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 760; Нарушение авторских прав?; Мы поможем в написании вашей работы!