Альтернативные методы расчета НЦФ

Метод прямого расчета НЦФ по частотной характеристики понятен и прост для применения. Недостаток метода – отсутствие гибкости. Он не позволяет проектировать фильтры с разной степенью неравномерности частотной характеристики в полосах пропускания и подавления, а степень неравномерности не зависит от количества членов фильтра и не может изменяться. Максимальные осцилляции частотной характеристики всегда наблюдаются в области полосовых границ и уменьшаются при удалении от них, но при близких границах могут наблюдаться явления интерференции осцилляций. Более гибкими в проектировании являются альтернативные методы: оптимизационные,

Оптимизационные методы позволяют проектировать экономные по размерам операторы фильтров с оптимальными (по Чебышеву) осцилляциями частотных характеристик. Они основаны на понятии полос равных колебаний.

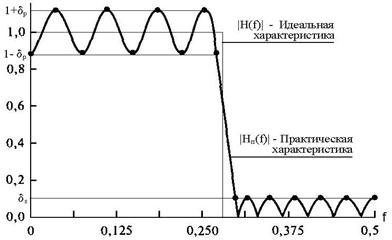Рис. 7.6.1. Оптимальный фильтр низких частот

Частотная характеристика оптимального фильтра низких частот приведена на рис. 7.6.1. В полосе пропускания реальная характеристика фильтра осциллирует с постоянными амплитудными колебаниями между значениями 1-d_p и 1+d_p. В полосе подавления осцилляции постоянной амплитуды находятся в интервале 0-d_s. Разность между идеальной и практической характеристиками представляет собой функцию ошибок E(f). Оптимальный метод позволяет определить коэффициенты фильтра h(n), для которых значение максимальной взвешенной ошибки минимизируется

min[max(E(f))]

в полосе пропускания и в полосе подавления, при этом характеристика фильтра будет иметь равные колебания в пределах полос пропускания и подавления, а количество экстремумов колебаний у фильтров с линейной фазовой характеристикой обычно прямо связано с количеством коэффициентов фильтра (N+1)/2.

При расчете фильтра ключевым моментом является определение положения частот экстремумов, которое выполняется итерационным алгоритмом Ремеза, после чего по положениям экстремумов задается частотная характеристика фильтра и определяются его коэффициенты. Методика расчета оптимальных фильтров подробно с примерами, в том числе в среде Matlab, рассмотрена в работе /43/.

Метод частотной выборки представляет собой вариант метода расчета фильтра по частотной характеристике без применения весовых функций и может применяться для расчетов как частотно-избирательных фильтров, так и фильтров с произвольной частотной характеристикой.

В основе метода лежит непосредственное задание частотной характеристики фильтра в цифровой форме с последующим подбором переходных зон под требуемые характеристики фильтра по величине допустимых осцилляций в полосе пропускания и подавления. Расчет желательно вести в интерактивном режиме, например, в среде Mathcad. В качестве примера приведем расчет низкочастотного фильтра.

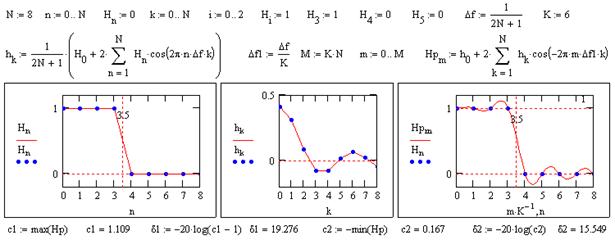Рис. 7.6.2. Задание параметров НЦФ.

Допустим, нам требуется достаточно простой симметричный низкочастотный фильтр с шириной переходной зоны порядка 0.2 главного частотного диапазона (при Dk=1 для фильтра, f_N = 0.5 Гц для спектра и ширина переходной зоны 0.2 х 0.5 = 0.1 Гц). Минимальный размер фильтра при идеальной характеристике для обеспечения такого перехода 2N+1 = 2(1+1/0.1) = 11 точек. С учетом расширения переходной зоны при уменьшении осцилляций на границе зон примем для начала N=8. Частотная характеристика проектируемого фильтра (правая половина) приведена на рис. 7.6.2 с границей раздела зон между 3 и 4 отсчетами спектра. Расчет оператора фильтра проводим обратным преобразованием Фурье, а по полученным отсчетам оператора вычисляем фактическую частотную характеристику этого оператора с уменьшением шага по частоте в 4-6 раз, что позволяет выявить осцилляции и определить погрешность фильтра (по максимумам осцилляций).

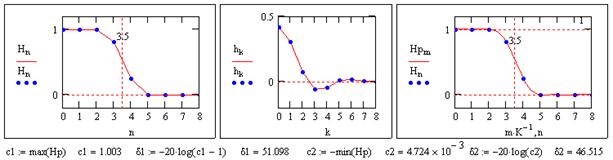Рис. 7.6.3. Подбор отсчетов переходной зоны НЦФ.

На рис. 7.6.3. показан результат подбора частотных значений характеристики фильтра в районе переходной зоны (2 точки), что позволяет более чем в 30 раз снизить осцилляции частотной характеристики.

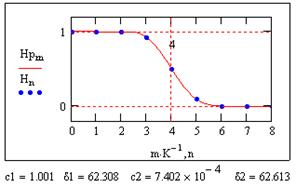Рис. 7.6.4. НЦФ с точкой подбора на границе.

Попутно заметим, что изменение осцилляций характеристики фильтра может производиться индивидуально для зоны пропускания (левой от границы точкой) и зоны подавления (правой точкой) в зависимости от того, требуется ли более высокая точность пропускания или подавления частот. Особенно эффективно это при использовании трех точек подбора с расположением центральной точки на границе полос пропускания и подавления, как это показано на рис. 7.6.4.

При использовании данного метода может использоваться и комбинированный подход: задание на частотной характеристике избыточного количества точек, отладка параметров фильтра по трем и более точкам в переходных зонах, а затем усечение оператора фильтра с применением весовых функций.

Метод частотных выборок допускает также рекурсивную реализацию фильтров.

литература

Хемминг Р.В. Цифровые фильтры. – М.: Недра, 1987. – 221 с.

Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход. / М., "Вильямс", 2004, 992 с.

Дата добавления: 2014-01-03