Свойства z-преобразования

Важнейшим свойством z-преобразования является свойство его единственности. Любая последовательность s(k) однозначно определяется z-изображением в области его сходимости, и наоборот, однозначно восстанавливается по z-изображению.

Без углубления в теорию, можно констатировать, что все свойства ДПФ действительны и для z-преобразования. Отметим некоторые из них.

Линейность: Если s(k) = a·x(k)+b·y(k), то S(z) = aX(z)+bY(z). Соответственно, z-преобразование допустимо только для анализа линейных систем и сигналов, удовлетворяющих принципу суперпозиции.

Задержка на n тактов: y(k) = x(k-n).

Y(z) =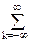y(k) z^k =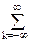x(k-n) z^k =zⁿ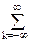x(k-n) z^k-n = zⁿ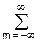x(m) z^m = zⁿ X(z).

Соответственно, умножение z-образа сигнала на множитель zⁿ вызывает сдвиг сигнала на n тактов дискретизации.

Преобразование свертки. При выполнении нерекурсивной цифровой фильтрации односторонними операторами фильтров:

s(k) =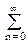h(n) y(k-n), k = 0, 1, 2, …

Z-преобразование уравнения свертки:

S(z) =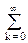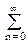h(n) y(k-n) z^k =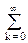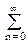h(n) zⁿ y(k-n) z^k-n =

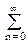=h(n) zⁿ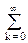y(k-n) z^k-n = H(z) Y(z).

Таким образом, свертка дискретных функций отображается произведением z-образов этих функций. Аналогично, для z-преобразования могут быть доказаны все известные теоремы о свойствах z-образов, что вполне естественно, т.к. при z=exp(-jw) эти свойства полностью эквивалентны свойствам спектров функций.

Разложение сигналов на блоки последовательной свертки. Z-преобразование позволяет производить разложение сигналов и функций, например передаточных функций фильтров, на короткие составляющие операции свертки, для чего достаточно приравнять z-полином к нулю, найти его корни a_i, и переписать полином в виде произведения двучленов:

S(z) = a₀(z-a₁)(z-a₂)...,

где а₀- последний отсчет сигнала (коэффициент при старшей степени z).

Но произведению в z-области соответствует свертка в координатной области, и при обратном преобразовании двучлены (z-a_i) превращаются в двухточечные диполи {-a_i,1}, а сигнал длиной N представляется сверткой (N-1) диполей:

s_k= a₀{-a₁,1}_*{-a₂,1}_*{-a₃,1}_*...

Пример. s_k = {1.4464, -2.32, 3.37, -3, 1}. S(z) = z⁴-3z³+3.37z²-2.32z+1.4464. a₀ = 1.

Корни полинома S(z): a₁ = 0.8+0.8j, a₂ = 0.8-0.8j, a₃ = 0.7+0.8j, a₄ = 0.7-0.8j,

S(z) = (z-0.8-0.8j)(z-0.8+0.8j)(z-0.7-0.8j)(z-0.7+0.8j).

Корни полинома представлены на z-плоскости на рис. 8.1.1. Корни полинома комплексные и четыре двучлена в координатной области также будут комплексными. Но они являются сопряженными, и для получения вещественных функций следует перемножить сопряженные двучлены и получить биквадратные блоки: S(z) = (z²-1.4z+1.13)(z²-1.6z+1.28).

При переходе в координатную область: s_k = {1.13, -1.4, 1} _* {1.28, -1.6, 1}.

Таким образом, исходный сигнал разложен на свертку двух трехчленных сигналов (функций).

Дифференцирование. Если имеем s(k) «S(z), то z-образ функции ks(k) можно найти, продифференцировав S(z), что бывает полезно для вычисления обратного z-преобразования функций S(z) с полюсами высокого порядка:

ks(k) «z dX(z)/dz.

Дата добавления: 2014-01-03