Обратное z-преобразование

Методы преобразования. Обратное z-преобразование позволяет восстанавливать дискретную функцию по ее z-образу. Оно широко используется, например, при определении импульсных характеристик рекурсивных цифровых фильтров. В символической форме:

x(k) = TZ^-1[X(z)].

На практике X(z) в процессе расчетов обычно выражается через отношение двух многочленов от z:

X(z) = (b₀ + b₁ z + b₂ z² + …+ b_N z^N) / (a₀ + a₁ z + a₂ z² + …+ a_M z^M) = (8.4.1)

= x(0) + x(1)z + x(2)z² + … (8.4.1')

Самые распространенные методы обратного преобразования из этой формы X(z):

• Преобразование интегрированием по контуру (метод вычетов).
• Метод разложения на элементарные дроби.
• Метод разложения в степенной ряд.

Метод разложения в степенной ряд наиболее прост и пригоден для выполнения на компьютерах, но он не дает решения в аналитической форме. При задании большого числа точек обратного преобразования требуется также следить за возможным нарастанием числовых ошибок вследствие рекурсии его алгоритма.

Два первых метода позволяют получать результаты в аналитическом виде, но требуют вычисления полюсов функции X(z), что может представлять трудности при высоком порядке функции. При высоких порядках полюсов потребуется также дифференцирование соответствующих порядков.

Преобразование интегрированием по контуру относится к числу математически строгих методов. Оно выполняется интегрированием по произвольному замкнутому контуру C, расположенному в области сходимости и окружающему все особые точки (нули и полюсы) z-образа. Интегрирование удобнее выполнять над полюсами, расположенными внутри контура, включающего центр системы координат, т.е. в символике z^-1. В этой символике мы и будем рассматривать данных параграф. Контурный интеграл обратного преобразования:

s_k = (1/2pj) 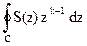. (8.4.2)

Согласно теореме Коши о вычетах, интеграл (8.4.2) равен сумме вычетов (Res) подынтегральной функции относительно всех полюсов этой функции, лежащих внутри контура интегрирования. Каждый вычет связан с определенным полюсом p_k:

Res[F(z), p_k] = 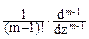[(z-p_k) F(z)] при z=p_k. (8.4.3)

где F(z) = z^k-1 S(z), m – порядок полюса в точке p_k. Для простого полюса:

Res[F(z), p_k] = (z-p_k) F(z) = (z-p_k) z^k-1 S(z) при z=p_k. (8.4.3')

Пример. Z-образ функции: X(z) = z² / (z-0.5)(z-1)².

x(k) = Res[F(z), p₁] + Res[F(z), p₂]. F(z) = z^k-1 X(z) = z^k+1 / (z-0.5)(z-1)².

Функция F(z) имеет простой полюс p₁ = 0.5 и полюс второго порядка p₂ = 1.

Res[F(z), 0.5] = (z-0.5) z^k+1 / (z-0.5)(z-1)² = z^k+1 / (z-1)² |_z=0.5 = 0.5 (0.5)^k / (0.5)² = 2(0.5)^k.

Res[F(z), 1] =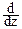[(z-1)² z^k+1 / (z-0.5)(z-1)²] = [(z-0.5)(k+1)z^k-z^k+1] / (z-0.5)² |_z=1= 2(k-1).

Результат: x(k) = 2[(k-1) + (0.5)^k].

Преобразование разложением на дроби. В этом методе z-образ (8.4.1) раскладывается на рациональные простые дроби с последующим почленным обратным преобразованием с помощью таблицы. Наиболее просто это выполняется, если функция S(z) может быть разложена по степеням z в символике z^-1, т.е. представить в следующем виде:

S(z) = s(0) + s(1) z^-1+ s(2) z^-2 + …

Соответственно, в выражении (8.4.1) отношение многочленов также должно быть в символике z^-1. Если полюсы S(z) первого порядка и N = M, то (8.4.1) можно разложить на следующую сумму:

S(z) = B₀ + C₁/(1-p₁z^-1) + C₂/(1-p₂z^-2) + … + C_M/(1-p_Mz^-M) =

B₀ + C₁z/(z-p₁) + C₂z/(z-p₂) + … + C_Mz/(z-p_M) = B₀ +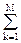C_kz/(z-p_k). (8.4.4)

B₀ = b_N / a_N.

где С_k – коэффициенты элементарных дробей, которые являются вычетами функции S(z).

Для вычисления коэффициентов C_k умножим левую и правую сторону выражения (8.4.4) на (z-p_k)/z и положим z=p_k, при этом в правой части за счет множителя (z-p_k)=0 при z=p_k обнуляются все члены суммы кроме члена с C_k данного полюса, а в левой остается произведение S(z)(z-p_k)/z, что и позволяет вычислить значения C_k:

C_k = S(z)(z-p_k)/z |_z=pk (8.4.5)

Если в (8.4.1) N < M, то значение B₀ равно нулю. Если функция S(z) в точке z=p_k имеет полюс m-ного порядка, то коэффициент C_k заменяется суммой коэффициентов:

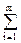D_i /(z-p_k)ⁱ, (8.4.6)

D_i = 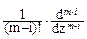[ X(z) (z-p_k)^m/z], при z=p_k. (8.4.7)

Пример. Повторим пример преобразования данным способом z-образа функции

X(z) = z² / (z-0.5)(z-1)², использованного в предыдущем примере. Функция имеет простой полюс p₁ = 0.5 и полюс второго порядка p₂ = 1.

X(z) = Cz/(z-0.5) + D₁z/(z-1) + D₂z/(z-1)².

С = z/(z-1)² = 0.5/(0.5-1)² = 2.

D₁ = 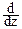[(z-1)² X(z)/z] = 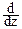[z / (z-0.5)] |_z=1= -2.

D₂ = (z-1)² X(z)/z = z/(z-0.5) |_z=1= 2.

X(z) = 2z/(z-0.5) + D₁z/(z-1) + D₂z/(z-1)².

Обратное преобразование каждой простой дроби выполним по таблице 8.2.1.

Результат: x(k) = 2(0.5)^k -2 +2k = 2[(k-1) + (0.5)^k]. Результат аналогичен методу вычетов.

Если z-изображение имеет вид дробно-рациональной функции, то разложение на простые дроби с последующим применением таблицы соответствий обычно труда не представляет. Так, например:

S(z) = (b₀ + b₁ z^-1 + b₂ z^-2) / (1 - a z^-1) = b₀/(1 - a z^-1) + b₁ z^-1/(1 - a z^-1) + b₂ z^-2/(1 - a z^-1).

По таблице соответствия:

X(z) = 1/(1-az^-1) → x(k) = a^k.

Отсюда, с учетом линейности преобразования и свойства задержки:

x(k) = b₀ a^k + b₁ a^k-1 + b₂ a^k-2.

При преобразовании функций со знаменателями более высоких порядков предварительно следует найти полюса функции. Например, для многочлена второго порядка с полюсами p₁ и p₂:

S(z) = 1/(1-a₁ z^-1+a₂ z^-2) = 1/[(1-p₁ z^-1)(1-p₂ z^-1).

Представим S(z) в виде суммы дробей с неизвестными коэффициентами b₁ и b₂:

S(z) = b₁/(1-p₁ z^-1)+b₂/(1-p₂ z^-1) = (b₁- b₁ p₂ z^-1+b₂-b₂ p₁ z^-1)/[(1-p₁ z^-1)(1-p₂ z^-1).

При равенстве знаменателей в этих двух выражениях должны быть равны и числители:

(b₁ + b₂) – (b₁ p₂+b₂ p₁)z^-1 = 1,

а это обеспечивается равенством коэффициентов при одинаковых степенях z. Отсюда получаем систему уравнений:

b₁ + b₂ = 1.

b₁ p₂+b₂ p₁ = 0.

Решая эту систему уравнений, находим значения коэффициентов b₁ и b₂, подставляем коэффициенты в S(z), выраженное в виде суммы дробей, и по таблице соответствия переводим дроби во временные функции.

Метод степенных рядов. Выражение (8.4.1) можно разложить непосредственно в степенной ряд (8.4.1') путем деления в столбик, для чего числитель и знаменатель функции выражаются предварительно через нарастающий или уменьшающийся показатель степени z. Обратное z-преобразование степенного ряда очевидно.

Пример нарастающей степени z. X(z) = (1+2z+z²) / (1-z+0.4z²).

1 + 2z + z² | 1 – z + 0.4z²

1 – z + 0.4z² 1 + 3z + 3.6z² + 2.4z³ + 0.96z⁴ + … Ряд может быть бесконечным.

3z + 0.6z²

3z – 3z² + 1.2z³

3.6z² – 1.2z³

3.6z² – 3.6z³ + 1.44z⁴

2.4z³ – 1.44z⁴

2.4z³ – 2.4z⁴ + 0.96z⁵

0.96z⁴ – 0.96z⁵

0.96z⁴ – 0.96z⁵ + 0.384z⁶, и т.д.

Обратное преобразование выполняется путем идентификации коэффициентов степеней при z^k с k-отсчетами функции: x(k) = {1, 3, 3.6, 2.4, 0.96, …}.

Пример уменьшающихся номеров степени z. X(z) = (1+2z+z²) / (1-z+0.4z²) → (деление на z^N числителя и знаменателя полинома) → (z^-2+2z^-1+1) / (z^-2-z^-1+0.4).

z^-2 + 2z^-1 + 1 | z^-2 – z^-1 + 0.4

z^-2 – z^-1 + 0.4 1 + 3z + 3.6z² + 2.4z³ + 0.96z⁴ + … Результат тот же.

3z^-1 + 0.6

3z^-1 – 3 + 1.2z

3.6 – 1.2z

3.6 – 3.6z + 1.44z²

2.4z – 1.44z²

2.4z – 2.4z² + 0.96z³

0.96z² – 0.96z³

0.96z² – 0.96z³ + 0.384z⁴, и т.д.

Метод деления полинома (8.4.1) можно выполнять рекурсивно:

x(0) = b₀ / a₀,

x(1) = (b₁ – x(0) a₁) / a₀,

x(2) = (b₂ – x(1) a₁ – x(0) a₂) / a₀,

…

x(n) = (b_n – 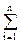(x(n-i) a_i) /a₀, n = 1, 2, 3, …

8.5. ПРИМЕНЕНИЕ Z – ПРЕОБРАЗОВАНИЯ.

Описание дискретных систем обработки сигналов с помощью нулей и полюсов - наиболее широкая область использования z-преобразования. Степенной полином передаточной функции системы вида (8.4.1) с нулями n_i числителя и полюсами p_j знаменателя всегда может быть представлен в виде произведения сомножителей:

H(z) = K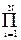(z-n_i) /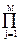(z-p_j), (8.5.1)

где К – коэффициент передачи (усиления) входного сигнала. Полюсы и нули H(z) могут быть действительными и комплексными, при этом для обеспечения действительных значений коэффициентов a_i и b_j в (8.4.1) комплексные коэффициенты должны быть представлены комплексно сопряженными парами.

Геометрическая оценка АЧХ и ФЧХ системы. Информацию, содержащуюся в H(z), удобно отображать в виде положения нулей (кружками) и полюсов (крестиками) на z-плоскости. Диаграмма нулей и полюсов наглядно отображает свойства системы и ее устойчивость. Для устойчивых систем все полюсы должны находиться за пределами единичной окружности (внутри окружности при символике z^-1) или совпадать с нулями на единичной окружности. На положение нулей ограничений не существует.

По известной диаграмме нулей и полюсов может быть выполнена геометрическая оценка частотной характеристики системы. При z=exp(-jwDt) единичная окружность |z|=1 отображает частотную ось характеристики главного частотного диапазона от w = 0 (z=1) до 2p (z=-1). Каждой точке z_s = exp(-jw_sDt) может быть поставлен в соответствие вектор (z_s – n_i) на i-нуль, модуль которого U_i = |(z_s – n_i)| отображает расстояние от z_s до i-нуля, а аргумент f_i = arg(z_s – n_i) - фазовый угол из z_s на i-нуль, а равно и вектор (z_s – p_j) на j-полюс с соответствующим расстоянием V_j = (z_s – p_j) и фазовым углом j_j = arg(z_s – p_j). При этом амплитудная и фазовая характеристики системы могут быть оценены по выражениям при перемещении точки w_s по единичной окружности:

|H(w)| = 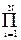U_i /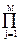V_j, (8.5.2)

arg(H(w)) = 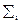f_i –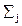j_j. (8.5.3)

По (8.5.2) нетрудно сделать заключение, что наибольшее влияние на изменение АЧХ по частоте оказывают нули и полюсы, расположенные ближе к единичной окружности. При расположении нуля непосредственно на окружности гармоника w_s в этой точке полностью обнуляется. И, наоборот, при перемещении w_s к полюсу, близкому к единичной окружности, происходит резкое нарастание коэффициента усиления системы.

Вычисление частотной характеристики с помощью БПФ. Так как частотная характеристика дискретной системы – это Фурье образ ее импульсной характеристики, то для систем, описанных в общей форме (8.4.1), сначала производится разложение H(z) в степенной ряд (8.4.1'), над коэффициентами которого и выполняется БПФ. Гладкость (разрешение по частоте Df = 1/(NDt)) будет определяться количеством коэффициентов степенного ряда и при необходимости может увеличиваться дополнением ряда нулями.

Альтернативный способ – вычисление БПФ непосредственно коэффициентов b_n числителя и a_m знаменателя выражения (8.4.1) с последующим алгебраическим делением B(k)/A(k) результатов БПФ. Количество коэффициентов b_n и a_n в (8.4.1) обычно невелико и для получения достаточно гладких частотных характеристик их продлевают нулями до необходимого значения N = 1/(DtDf).

Анализ устойчивости систем выполняется для рекурсивных систем с бесконечной импульсной характеристикой (БИХ-систем). Такие системы описываются либо непосредственно в виде разностного уравнения, либо передаточной функцией в виде z-образа импульсной характеристики или разностного уравнения. Общее условие устойчивости импульсной характеристики системы:

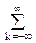|h(k)| < ∞.

Для рекурсивных систем начальный индекс суммирования равен нулю. Практически это означает, что любой ограниченный входной сигнал в устойчивой системе порождает ограниченный выходной сигнал.

В устойчивой системе все полюсы передаточной функции H(z) должны находиться за границами единичной окружности z=exp(-jwDt) (внутри окружности при символике z^-1). Система с полюсом на единичной окружности также считается неустойчивой (потенциально неустойчивой), даже если во входном сигнале нет гармоники с частотой, соответствующей положению данного полюса на окружности. Это определяется тем, что в соответствии с (8.5.1) коэффициент усиления системы в точке полюса равен бесконечности и любой бесконечно малый сигнал на этой частоте даст бесконечно большой сигнал на выходе. Естественно, что для практических систем понятия бесконечности не существует и можно пытаться принять определенные меры для исключения таких критических частот. Так, например, в интегрирующих системах полюс находится на нулевой частоте и из входного сигнала можно исключить постоянную составляющую, но при этом изменяется и характер интегрирования (только динамические составляющие входного сигнала). Следует также учитывать, что во входных сигналах обычно всегда присутствует определенный статистический шум, наблюдаются скачки, присутствует шум квантования и т.п. эффекты с непрерывным частотным спектром, которые могут приводить к огромным ошибкам при обработке данных в потенциально неустойчивых системах. Практически осуществимый способ повышения устойчивости систем – компенсировать полюсы на окружности нулями в этих же точках, но это может приводить к существенному изменению частотной характеристики системы.

Оценку устойчивости рекурсивной системы можно проводить и по виду ее импульсной характеристики (вычислением обратного z-преобразования или подачей импульса Кронекера на вход (алгоритм) системы). Если значения коэффициентов увеличиваются по мере роста номеров – система неустойчива. Если они очень медленно уменьшаются (медленно стремятся к нулю) – система устойчива минимально, имеет большое время установления рабочего режима, при определенных условиях может давать большие погрешности в обрабатываемых данных.

Связь разностных уравнений и передаточных функций рекурсивных систем. Стандартная запись разностного уравнения системы (связи входного воздействия x(k) и выходного сигнала y(k) при известных постоянных параметрах нерекурсивной b_n и рекурсивной a_m трансформации сигналов):

y(k) = 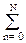b_n x(k-n) -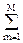a_m y(k-m). (8.5.4)

От разностного уравнения с использованием свойства задержки z-преобразования

b_n x(k) «b_n X(z),

b_n x(k-n) «b_n zⁿ X(z),

нетрудно перейти к z-образу разностного уравнения системы:

Y(z) = 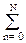b_n X(z) zⁿ -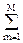a_m Y(z) z^m. (8.5.5)

Отсюда, передаточная функция системы:

Y(z) (1+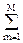a_m z^m) =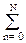b_n X(z) zⁿ.

H(z) = Y(z) / X(z) = 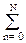b_n zⁿ /(1+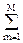a_m z^m). (8.5.6)

И, наоборот, при приведении выражения (8.4.1) к виду (8.5.6) (нормировкой на a₀) можно без дальнейших преобразований переходить к выражению (8.5.4).

Пример. Передаточная функция: H(z) = 2(1-z) / (2+z). Определить алгоритм вычислений.

H(z) = Y(z)/X(z) = (1-z) / (1+0.5z).

Y(z) + 0.5 z Y(z) = X(z) – z X(z).

y(k) + 0.5 y(k-1) = x(k) – x(k-1)

Результат: y(k) = x(k) – x(k-1) - 0.5 y(k-1)

литература

Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Высшая школа, 1988.- 448 с. (с. 388-391)

Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.

Канасевич Э.Р. Анализ временных последовательностей в геофизике. - М.: Недра, 1985.- 300 с.

Рапопорт М.Б. Вычислительная техника в полевой геофизике: Учебник для вузов. - М.: Недра, 1993.- 350 с.

Новиков Л.В. Основы вейвлет-анализа сигналов. Учебное пособие. СПб, ИАнП РАН, 1999.

Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход. / М., "Вильямс", 2004, 992 с.

Дата добавления: 2014-01-03