Общие сведения об адаптивной цифровой фильтрации

Основные области применения адаптивной фильтрации – очистка данных от нестабильных мешающих сигналов и шумов, перекрывающихся по спектру со спектром полезных сигналов, или когда полоса мешающих частот неизвестна, переменна и не может быть задана априорно для расчета параметрических фильтров. Так, например, в цифровой связи сильная активная помеха может интерферировать с полезным сигналом, а при передаче цифровой информации по каналам с плохими частотными характеристиками может наблюдаться межсимвольная интерференция цифровых кодов. Эффективное решение этих проблем возможно только адаптивными фильтрами.

Частотная характеристика адаптивных фильтров автоматически регулируется или модифицируется в соответствии с определенным критерием, позволяющем фильтру адаптироваться к изменениям характеристик входного сигнала. Они достаточно широко используются в радио- и гидролокации, в системах навигации, в выделении биомедицинских сигналов, и многих других отраслях техники. В качестве примера рассмотрим наиболее распространенные схемы адаптивной фильтрации сигналов.

Адаптивный шумоподавитель. Блок-схема фильтра приведена на рис. 11.1.1.

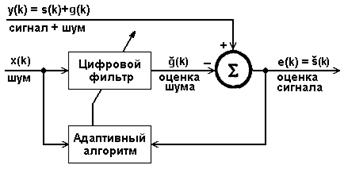Рис. 11.1.1.

Фильтр состоит из блока цифрового фильтра с регулируемыми коэффициентами и адаптивного алгоритма для настройки и изменения коэффициентов фильтра. На фильтр одновременно подаются входные сигналы y(k) и x(k). Сигнал y(k) содержит полезный сигнал s(k) и некоррелированный с ним загрязняющий сигнал g(k). Сигнал x(k) какого-либо источника шума, коррелированный с g(k), который используется для формирования оценки сигнала ğ(k). Полезный сигнал оценивается по разности:

š(k) = y(k) – ğ(k) = s(k) + g(k) – ğ(k). (11.1.1)

Возводим уравнение в квадрат и получаем:

š²(k) = s²(k) + (g(k) – ğ(k))² + 2.s(k) (g(k) – ğ(k)). (11.1.2)

Вычислим математическое ожидание левой и правой части этого уравнения:

M[š²(k)] = M[s²(k)] + M[(g(k) – ğ(k))²] + 2M[s(k) (g(k) – ğ(k))]. (11.1.3)

Последнее слагаемое в выражении равно нулю, поскольку сигнал s(k) не коррелирует с сигналами g(k) и ğ(k).

M[š²(k)] = M[s²(k)] + M[(g(k) – ğ(k))²]. (11.1.4)

В этом выражении M[s²(k)] = W(s(k)) – мощность сигнала s(k), M[š²(k)] = W(š(k)) – оценка мощности сигнала s(k) и общая выходная мощность, M[(g(k) – ğ(k))²] = W(e_g) - остаточная мощность шума, который может содержаться в выходном сигнале. При настройке адаптивного фильтра к оптимальному положению минимизируется мощность остаточного шума, а, следовательно, и мощность выходного сигнала:

min W(š(k)) = W(s(k)) + min W(e_g). (11.1.5)

На мощность полезного сигнала настройка не влияет, поскольку сигнал не коррелирован с шумом. Эффект минимизации общей выходной мощности будет выражаться в максимизации выходного отношения сигнал/шум. Если настройка фильтра обеспечивает равенство ğ(k) = g(k), то при этом š(k) = s(k). Если сигнал не содержит шума, адаптивный алгоритм должен устанавливать нулевые значения всем коэффициентам цифрового фильтра.

Рис. 11.1.2.

Адаптивный фильтр Винера. Входной сигнал y(k) фильтра, приведенного на рис. 11.1.2, включает компоненту, коррелированную с со вторым сигналом x(k), и полезную компоненту, некоррелированную с x(k). Фильтр формирует из x(t) сигнал ğ(k) - оптимальную оценку той части у(k), которая коррелированна с x(k), и вычитает ее из сигнала y(k). Выходной сигнал:

e(k) = y(k) - ğ(k) = y(k) - H ^T X _k = y(k) -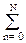h(n) x(k-n),

где H ^T и X _k – векторы весовых коэффициентов фильтра и его входного сигнала.

Аналогично предыдущему методу, возводим в квадрат левую и правую части уравнения, находим математические ожидания обеих частей и получаем уравнение оптимизации e выходного сигнала:

e = s² + 2 P ^T H + H ^T RH, (11.1.6)

где s² = M[y²(k)] – дисперсия y(k), P = M[y(k) X _k] – вектор взаимной корреляции, R = M[ X _k X _k^T] – автокорреляционная матрица.

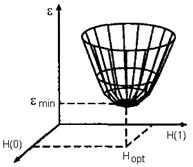Рис. 11.1.3.

В стационарной среде график зависимости e от коэффициентов H представляет собой чашеобразную поверхность адаптации (рис. 11.1.3). Градиент поверхности:

D = de / d H = -2 P + 2 RH.

Каждому набору коэффициентов h(n) на этой поверхности соответствует определенная точка. В точке минимума градиент равен нулю и вектор весовых коэффициентов фильтра является оптимальным:

H _opt = R ^-1 P. (11.1.7)

Эта формула называется уравнением Винера-Хопфа. Задачей алгоритма автоматической настройки является подбор таких весовых коэффициентов фильтра, которые обеспечивают работу в оптимальной точке поверхности адаптации.

Однако практическое применение фильтра затрудняется использованием корреляционных матриц R и P, априори неизвестных, и которые могут изменяться со временем для нестационарных сигналов.

Адаптивный алгоритм наименьших квадратов Уидроу-Хопфа. По существу, это модификация фильтра Винера, в которой вместо вычисления коэффициентов (11.1.7) за один шаг используется алгоритм последовательного спуска в оптимальную точку при обработке каждой выборки:

H _k+1 = H _k - me_k X _k, (11.1.8)

e_k = y_k - H ^T X _k. (11.1.9)

Условие сходимости к оптимуму:

0 < m > 1/l_max, (11.1.10)

где m - параметр скорости спуска, l_max – максимальное собственное значение ковариационной матрицы данных. Блок-схема алгоритма приведена на рис. 11.1.4.

Рис. 11.1.4. Алгоритм адаптации методом наименьших квадратов.

На практике точка максимальной оптимальности флюктуирует около теоретически возможной. Если входной сигнал нестационарный, то изменение статистик сигнала должно происходить достаточно медленно, чтобы коэффициенты фильтра успевали следить за этими изменениями.

Рекурсивные схемы наименьших квадратов отличаются тем, что вычисление каждой последующей выборки коэффициентов h(n) производится не только по коэффициентам только одной предыдущей выборки, но и с определенной длиной постепенно затухающей памяти по предшествующим выборкам, что позволяет снижать флюктуации оценок при обработке стационарных сигналов.

Дата добавления: 2014-01-03