Инверсия импульсного отклика фильтра

Вычисление коэффициентов инверсного фильтра по значениям каузального (одностороннего) оператора h(n) может быть проведено на основе выражения (13.1.3):

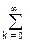h^-1(k)h(n-k) = d_o(n), (13.2.1)

для чего достаточно развернуть его в систему n-уравнений при n = 0, 1, 2, …, k ≤ n:

n = 0: h^-1(0)h(0) = 1, h^-1(0) = 1/h(0).

n = 1: h^-1(0)h(1)+h^-1(1)h(0) = 0, h^-1(1) = h^-1(0)h(1) / h(0).

n = 2: h^-1(0)h(2)+h^-1(1)h(1)+h^-1(2)h(0) = 0, h^-1(2) = (h^-1(0)h(2)+h^-1(1)h(1))/h(0), и т.д.

Продолжая последовательно, можно вычислить любое количество значений коэффициентов инверсного фильтра. Рекуррентная формула вычислений:

h^-1(n) = (1/h₀)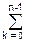h^-1(k)h(n-k). (13.2.2)

Если фильтр деконволюции устойчив и ряд h^-1(n) сходится, то появляется возможность ограничения количества членов ряда с определенной ошибкой восстановления исходного сигнала. Метрика приближения Е (квадратичная норма разности) определяется выражением:

Е² =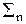[d_o(n) - h(n) ③ h^-1(n)]². (13.2.3)

Ошибка восстановления исходного сигнала появляется со сдвигом на длину оператора фильтра деконволюции и проявляется на интервале длины прямого оператора.

Пример инверсии оператора фильтра h_n = {0.219, 0.29, 0.257, 0.153, 0.061, 0.016, 0.003}.

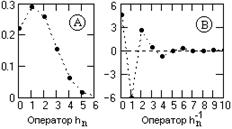Рис. 13.2.1.

Полином по zⁿ: H(z) = S_n h_n zⁿ.

Модули корней полинома: z_n = {2.054, 2.054, 2.485, 2.485, 1.699, 1.699}.

Модули корней больше 1, инверсный фильтр устойчив и, судя по значениям корней (достаточно существенно отличаются от 1), быстро затухает.

Двенадцать значений оператора по (13.2.2): h^-1(n) = {4.56, -6.033, 2.632, 0.417, -0.698, -0.062, 0.267, -0.024, -0.11, 0.051, 0.018, -0.019, 0.004}.

Значения прямого и инверсного оператора фильтра приведены на рис. 13.2.1.

Значения свертки прямого оператора с инверсным при длине N=10 инверсного фильтра и метрика приближения: s_n={1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.004, 0.006, 0.004, 0.002, <0.001, …}. E=0.0086.

На рис. 13.2.2 приведены графики абсолютных значений концевой ошибки деконволюции при разной длине N оператора деконволюции.

Рис. 13.2.2.

Дата добавления: 2014-01-03